在□ABCD中，AB=3，BC=4，则□ABCD的周长等于_______.
14
【解析】【解析】
∵四边形ABCD是平行四边形，∴CD=AB=3，AD=BC=4，∴?ABCD的周长为14．
故答案为：14． 平行四边形的周长等于56 cm，两邻边长的比为3∶1，那么这个平行四边形较长的边长为_______.
21cm
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB=CD，AD=BC．
∵平行四边形的周长等于56cm，∴AB+CD+AD+BC=56cm，∴AB+BC=28cm．
∵BC：AB=3：1，∴BC=21cm，AB=7cm，∴这个平行四边形较长的边长为21cm．
故答案为：21cm． 在□ABCD中，∠A+∠C=270°，则∠B=______，∠C=______.
45° 135°
【解析】【解析】
∵已知平行四边形ABCD，∴∠A=∠C，∠B+∠C=180°．
又∵∠A+∠C=270°，∴2∠C=270°，∠C=135°，∴∠B=180°-∠C=180°-135°=45°．
故答案为：∠C=135°，∠B=45°． 和直线l距离为8 cm的直线有______条.
2
【解析】【解析】
在同一平面上，和直线l距离为8cm的直线在直线L的两侧各有一条．故答案为：2． 在△ABC中，AB＝8 ㎝，AC＝10 ㎝，P，G，H分别是AB，BC，CA的中点，则四边形APGH的周长是______ ．
18cm
【解析】【解析】
∵P、G、H分别是AB、BC、CA的中点，∴PG、HG为△ABC的中位线，∴AP=AB=×8=4cm，AH=AC=×10=5cm，∴PG∥AC，GH∥AB，∴四边形APGH为平行四边形，HG=AP=4cm，PG=AH=5cm，∴四边形APGH的周长是（4+5）×2=18cm．
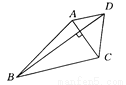
故答案为：18cm． 如图所示，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC＝5 ㎝， BD＝12 ㎝，则该梯形的两底之和等于____㎝．
13
【解析】【解析】
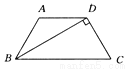
过点D作DE∥AC交BC的延长线于E，则DE与AC平行且相等，AD=CE．∵AC⊥BD，∴BD⊥DE．在Rt△BDE中，BE==13，∴BC+AD=13． 如图所示，在梯形ABCD中．AD∥BC，AB＝DC，BD⊥DC于点D，且∠C＝60°．若AD＝5㎝．则梯形的腰长为________㎝．
5
【解析】【解析】
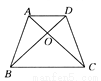
∵BD⊥DC于D，且∠C=60°，∴∠DBC=30°．∵AD∥BC，AB=DC，∴∠ABC=∠C=60°，∴∠ADB=∠DBC=∠ABD=30°，∴AB=AD=5cm．故答案为：5． 如图所示，在四边形ABCD中，已知AB与 CD不平行，∠ABD＝∠ACD，请你添加一个条件：______ ，使的加上这个条件后能够推出AD∥BC ，且AB＝CD．
∠DAC＝∠ADB或∠BAD＝∠CDA或∠DBC＝∠ACB或∠ABC＝∠DCB或OB＝OC或OA＝OD.
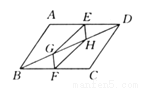
【解析】试题分析：先证四边形AECO是梯形，再说明是等腰梯形．由题意可知，∠ABD=∠ACD，AD是△BAD和△CDA的公共边，则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA，同理可添加∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD，从而推出AD∥BC且AB=C... 如图所示，E，F分别为平行四边形ABCD中AD，BC的中点，G，H在BD上，且 BG＝DH，求证四边形EGFH是平行四边形．
答案见解析
【解析】试题分析：由四边形ABCD是平行四边形，得到AD=BC，AD∥BC，由AD∥BC，得到∠ADB=∠DBC，因为E、F分别为?ABCD的边AD、BC的中点，得到DE=BF，由三角形全等证得EH=FG，∠EHD=∠FGB，得到EH∥FG，证出四边形FGEH是平行四边形．
试题解析：证明：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠ADB=∠DBC．∵E、... 如图所示，△ABC中AD⊥BC，E，F，G分别为BC，AB，AC的中点．求证四边形DEFG是等腰梯形．
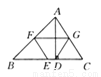
答案见解析
【解析】试题分析：因为G，F分别是AB，AC的中点，所以GF∥DE，则四边形DEFG是梯形．在Rt△ABD中，G为AB的中点，则DG=AB．而E，F分别是BC，AC的中点，则EF=AB，所以DG=EF，所以四边形DEFG是等腰梯形．
试题解析：证明：∵G，F分别是AB，AC的中点，∴GF∥DE，易得EF不平行于DG，∴四边形DEFG是梯形．在Rt△ABD中，G为AB的中点，...