题目内容
和直线l距离为8 cm的直线有______条.
 2
【解析】【解析】
在同一平面上,和直线l距离为8cm的直线在直线L的两侧各有一条.故答案为:2.
2
【解析】【解析】
在同一平面上,和直线l距离为8cm的直线在直线L的两侧各有一条.故答案为:2.
练习册系列答案
相关题目
已知多项式x2+a能用平方差公式在有理数范围内分解因式,那么在下列四个数中a可以等于( )
A. 9 B. 4
C. -1 D. -2
 C
【解析】当x=-1时,x2-1=(x+1)(x-1),其它的三个选项都不符合要求,故选C.
C
【解析】当x=-1时,x2-1=(x+1)(x-1),其它的三个选项都不符合要求,故选C. 若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为 ( )
A. x1=-3,x2=-1 B. x1=1,x2=3 C. x1=-1,x2=3 D. x1=-3,x2=1
 C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3.
C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3. 不等式组 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
A. 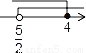 B.
B. 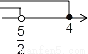 C.
C. 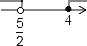 D.
D. 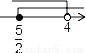
 A
【解析】解不等式x-1≤7-x得x≤4;
解不等式5x-2>3(x+1)得x>,
所以<x≤4.
在数轴上表示正确的是A.
故选A.
A
【解析】解不等式x-1≤7-x得x≤4;
解不等式5x-2>3(x+1)得x>,
所以<x≤4.
在数轴上表示正确的是A.
故选A. 如图所示,E,F分别为平行四边形ABCD中AD,BC的中点,G,H在BD上,且 BG=DH,求证四边形EGFH是平行四边形.
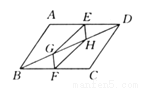
 答案见解析
【解析】试题分析:由四边形ABCD是平行四边形,得到AD=BC,AD∥BC,由AD∥BC,得到∠ADB=∠DBC,因为E、F分别为?ABCD的边AD、BC的中点,得到DE=BF,由三角形全等证得EH=FG,∠EHD=∠FGB,得到EH∥FG,证出四边形FGEH是平行四边形.
试题解析:证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC.∵E、...
答案见解析
【解析】试题分析:由四边形ABCD是平行四边形,得到AD=BC,AD∥BC,由AD∥BC,得到∠ADB=∠DBC,因为E、F分别为?ABCD的边AD、BC的中点,得到DE=BF,由三角形全等证得EH=FG,∠EHD=∠FGB,得到EH∥FG,证出四边形FGEH是平行四边形.
试题解析:证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC.∵E、... 在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AE, 则∠BAD等于 ( )
A. 120° B. 135° C. 130° D. 不能确定
 B
【解析】【解析】
过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B.
B
【解析】【解析】
过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B. 平行四边行的两条对角线把它分成全等三角形的对数是( )
A. 2 B. 4 C. 6 D. 8
 B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B.
B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B. 在□ABCD中,AB≠AD,满足下列条件,不一定能构成平行四边形的是( )
A. 四个内角平分线围成的四边形
B. 过四个顶点作对边的高线围成的四边形
C. 以对角线的交点把对角线分成的四部分的中点为顶点的四边形
D. 以一条对角线上的两点,与另两个顶点为顶点的四边形.
 D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D.
D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D. 如图,在△ABC和△ADC中,下列论断:①AB=AD;②∠ABC=∠ADC=90°;③BC=DC.把其中两个论断作为条件,另一个论断作为结论,可以写出_个真命题.
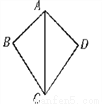
 2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2.
2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2. 
