题目内容
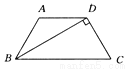
如图所示，在梯形ABCD中．AD∥BC，AB＝DC，BD⊥DC于点D，且∠C＝60°．若AD＝5㎝．则梯形的腰长为________㎝．
5
【解析】【解析】
∵BD⊥DC于D，且∠C=60°，∴∠DBC=30°．∵AD∥BC，AB=DC，∴∠ABC=∠C=60°，∴∠ADB=∠DBC=∠ABD=30°，∴AB=AD=5cm．故答案为：5．
练习册系列答案
阅读快车系列答案
相关题目
分解因式：x2－4＝_____.
(x+2) (x-2)
【解析】试题解析：x2-4=（x+2）（x-2）． 二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=﹣1，有以下结论：①abc＞0；②4ac＜b2；③2a+b=0；④a﹣b+c＞2．其中正确的结论的个数是（ ）
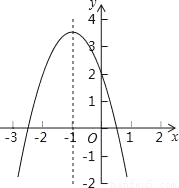
A. 1 B. 2 C. 3 D. 4
C
【解析】①∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x==﹣1，∴b=2a＜0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＞0，所以①正确；
②∵抛物线与x轴有2个交点，∴△=b2-4ac＞0，∴4ac 已知四个有理数a，b，x，y同时满足以下关系式：b＞a，x+y=a+b，y﹣x＜a﹣b．请将这四个有理数按从小到大的顺序用“＜”连接起来是 ．
y＜a＜b＜x
【解析】试题分析：由x+y=a+b得出y=a+b﹣x，x=a+b﹣y，求出b＜x，y＜a，即可得出答案．
∵x+y=a+b， ∴y=a+b﹣x，x=a+b﹣y， 把y=a=b﹣x代入y﹣x＜a﹣b得：a+b﹣x﹣x＜a﹣b，
2b＜2x， b＜x①， 把x=a+b﹣y代入y﹣x＜a﹣b得：y﹣（a+b﹣y）＜a﹣b，
2y＜2a， y＜a②， ∵b＞a③， ... 如图所示，在△ABC中，∠ACB＝90°点E是AB的中点，连接CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF＝CE，求证四边形ACEF是平行四边形．
答案见解析
【解析】试题分析：要证明四边形ACEF是平行四边形，需求证CE∥AF，由已知易得△BEC，△AEF是等腰三角形，则∠1=∠2，∠3=∠F，又∠2=∠3，得到∠1=∠F，故CE∥AF，由此即可得到结论．
试题解析：证明：∵点E为AB中点，∴AE=EB．又∵∠ACB=90°，∴CE=AE=EB．又∵AF=CE，∴AF=AE，∴∠3=∠F．又∵EB=EC，ED⊥BC，∴∠1=∠2... 平行四边形的周长等于56 cm，两邻边长的比为3∶1，那么这个平行四边形较长的边长为_______.
21cm
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB=CD，AD=BC．
∵平行四边形的周长等于56cm，∴AB+CD+AD+BC=56cm，∴AB+BC=28cm．
∵BC：AB=3：1，∴BC=21cm，AB=7cm，∴这个平行四边形较长的边长为21cm．
故答案为：21cm． 如图，平行四边形ABCD中，EF过对角线的交点O，AB＝4，AD＝3，OF＝1.3，则四边形BCEF的周长为（ ）
A. 8.3 B. 9.6 C. 12.6 D. 13.6
B
【解析】【解析】
根据平行四边形的中心对称性得：OF=OE=1.3．∵?ABCD的周长=（4+3）×2=14
∴四边形BCEF的周长=×?ABCD的周长+2.6=9.6．故选B． 若四边形ABCD中，AD＝BC，AC是对角线，且∠CAD＝∠ACB，则这个四边形是________．
平行四边形
【解析】【解析】
∵∠CAD＝∠ACB，∴AD∥BC．∵AD=BC，∴ABCD是平行四边形．故答案为：平行四边形． 一个多边形的内角度数从小到大排列起来，恰好依次增加相同的度数，其中最小角是
，最大角是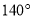
,求这个多边形的边数.
6
【解析】本题考查的是多边形的性质
根据“依次增加相同的度数，其中最小角是，最大角是”即可解得结果，注意边数为正整数。
设多边形的边数是，依次增加，
则
解得符合题意的正整数解
答：这个多边形的边数为