题目内容
平行四边形的周长等于56 cm,两邻边长的比为3∶1,那么这个平行四边形较长的边长为_______.
 21cm
【解析】【解析】
∵四边形ABCD是平行四边形,∴AB=CD,AD=BC.
∵平行四边形的周长等于56cm,∴AB+CD+AD+BC=56cm,∴AB+BC=28cm.
∵BC:AB=3:1,∴BC=21cm,AB=7cm,∴这个平行四边形较长的边长为21cm.
故答案为:21cm.
21cm
【解析】【解析】
∵四边形ABCD是平行四边形,∴AB=CD,AD=BC.
∵平行四边形的周长等于56cm,∴AB+CD+AD+BC=56cm,∴AB+BC=28cm.
∵BC:AB=3:1,∴BC=21cm,AB=7cm,∴这个平行四边形较长的边长为21cm.
故答案为:21cm.
练习册系列答案
相关题目
下列各式中,能用平方差公式因式分解的是( )
A. x2+x B. x2+8x+16 C. x2+4 D. x2﹣1
 D
【解析】A. x²+x=x(x+1),是提取公因式法分解因式,故此选项错误;
B. x²+8x+16=(x+4)²,是公式法分解因式,故此选项错误;
C. x²+4,无法分解因式,故此选项错误;
D. x²?1=(x+1)(x?1),能用平方差公因式分解,故此选项正确。
故选:D.
D
【解析】A. x²+x=x(x+1),是提取公因式法分解因式,故此选项错误;
B. x²+8x+16=(x+4)²,是公式法分解因式,故此选项错误;
C. x²+4,无法分解因式,故此选项错误;
D. x²?1=(x+1)(x?1),能用平方差公因式分解,故此选项正确。
故选:D. 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 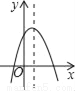 B.
B. 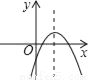 C.
C. 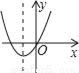 D.
D. 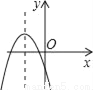
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B. 不等式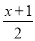 >
> -1的正整数解的个数是( )
-1的正整数解的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
 D
【解析】根据不等式的解法,去分母,得3(x+1)>2(2x+2)-6,去括号得3x+3>4x+4-6,移项合并同类项,x<5,可得其正整数解为1、2、3、4,共4个.
故选:D.
D
【解析】根据不等式的解法,去分母,得3(x+1)>2(2x+2)-6,去括号得3x+3>4x+4-6,移项合并同类项,x<5,可得其正整数解为1、2、3、4,共4个.
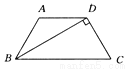
故选:D. 如图所示,在梯形ABCD中.AD∥BC,AB=DC,BD⊥DC于点D,且∠C=60°.若AD=5㎝.则梯形的腰长为________㎝.
 5
【解析】【解析】
∵BD⊥DC于D,且∠C=60°,∴∠DBC=30°.∵AD∥BC,AB=DC,∴∠ABC=∠C=60°,∴∠ADB=∠DBC=∠ABD=30°,∴AB=AD=5cm.故答案为:5.
5
【解析】【解析】
∵BD⊥DC于D,且∠C=60°,∴∠DBC=30°.∵AD∥BC,AB=DC,∴∠ABC=∠C=60°,∴∠ADB=∠DBC=∠ABD=30°,∴AB=AD=5cm.故答案为:5. 下列不能作为判定四边形ABCD为平行四边形的条件的是( )
A. AB=CD,AD=BC B. AB CD
CD
C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
 C
【解析】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故本选项合题意;
D.∵AB∥CD,AD∥BC,四边...
C
【解析】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故本选项合题意;
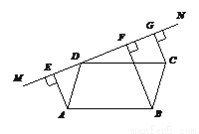
D.∵AB∥CD,AD∥BC,四边... 如图,直线MN过□ABCD的顶点D,过A,B,C三点,分别作MN的垂线,垂足分别是E,F,G.
求证:DE=FG.
 答案见解析
【解析】试题分析:作CH⊥BF与H.可证△AED≌△BHC,得到ED=HC,再由平行线间的距离处处相等得到FG=CH,即可得到结论.
试题解析:证明:作CH⊥BF与H.
∵AE⊥MN,BF⊥MN,∴AE∥BF,∴∠EAD+∠DAB+∠ABF=180°.
∵ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠DAB+∠ABF+∠HBC=180°,∴∠EAD=∠HB...
答案见解析
【解析】试题分析:作CH⊥BF与H.可证△AED≌△BHC,得到ED=HC,再由平行线间的距离处处相等得到FG=CH,即可得到结论.
试题解析:证明:作CH⊥BF与H.
∵AE⊥MN,BF⊥MN,∴AE∥BF,∴∠EAD+∠DAB+∠ABF=180°.
∵ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠DAB+∠ABF+∠HBC=180°,∴∠EAD=∠HB... 一个四边形的三个内角的度数依次如下,那么其中是平行四边形的是( )
A. 88°,108°,88° B. 88°,104°,88°
C. 88°,92°,92° D. 88°,92°,88°
 D
【解析】当三个内角度数依次是88°,108°,88°时,第四个角是76°,故A不是;
两组对角分别相等的四边形是平行四边形,故B不是;
当三个内角度数依次是88°,92°,92°时,第四个角是88°,而C中相等的两个角不是对角故C错,
D中满足两组对角分别相等,因而是平行四边形。
故选:D.
D
【解析】当三个内角度数依次是88°,108°,88°时,第四个角是76°,故A不是;
两组对角分别相等的四边形是平行四边形,故B不是;
当三个内角度数依次是88°,92°,92°时,第四个角是88°,而C中相等的两个角不是对角故C错,
D中满足两组对角分别相等,因而是平行四边形。
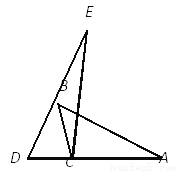
故选:D. 如图,点D,C,A在同一条直线上,在△ABC中,∠A∶∠ABC∶∠ACB=3∶5∶10,若△EDC≌△ABC,则∠BCE的度数为_.
 20°
【解析】利用三角形的三角的比∠A:∠ABC:∠ACB=3:5:10,设∠A=3x°,则∠ABC=5x°,∠ACB=10x°,根据三角形的内角和为180°得3x+5x+10x=180,解得x=10,求出三角的度数∠A=30°,∠ABC=50°,∠ACB=100°,可得∠BCN=180°-100°=80°,再由△MNC≌△ABC得到∠ACB=∠MCN=100°,因此可求得∠BCM=∠NC...
20°
【解析】利用三角形的三角的比∠A:∠ABC:∠ACB=3:5:10,设∠A=3x°,则∠ABC=5x°,∠ACB=10x°,根据三角形的内角和为180°得3x+5x+10x=180,解得x=10,求出三角的度数∠A=30°,∠ABC=50°,∠ACB=100°,可得∠BCN=180°-100°=80°,再由△MNC≌△ABC得到∠ACB=∠MCN=100°,因此可求得∠BCM=∠NC... 
