题目内容
如图所示,在四边形ABCD中,已知AB与 CD不平行,∠ABD=∠ACD,请你添加一个条件:______ ,使的加上这个条件后能够推出AD∥BC ,且AB=CD.
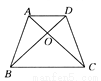
 ∠DAC=∠ADB或∠BAD=∠CDA或∠DBC=∠ACB或∠ABC=∠DCB或OB=OC或OA=OD.
【解析】试题分析:先证四边形AECO是梯形,再说明是等腰梯形.由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA,同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=C...
∠DAC=∠ADB或∠BAD=∠CDA或∠DBC=∠ACB或∠ABC=∠DCB或OB=OC或OA=OD.
【解析】试题分析:先证四边形AECO是梯形,再说明是等腰梯形.由题意可知,∠ABD=∠ACD,AD是△BAD和△CDA的公共边,则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA,同理可添加∠DBC=∠ACB,∠ABC=∠DCB,OB=OC,OA=OD,从而推出AD∥BC且AB=C...
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
已知|x﹣y+2|+ =0,则x2﹣y2的值为______.
=0,则x2﹣y2的值为______.
 ﹣4
【解析】因为|x?y+2|+=0,∴x?y+2=0,x+y?2=0,
∴x?y=?2,x+y=2,∴x²?y²=(x?y)(x+y)=?4.
故答案为:?4.
﹣4
【解析】因为|x?y+2|+=0,∴x?y+2=0,x+y?2=0,
∴x?y=?2,x+y=2,∴x²?y²=(x?y)(x+y)=?4.
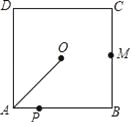
故答案为:?4. 如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( ).
A. 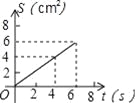 B.
B. 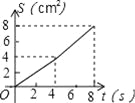
C. 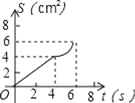 D.
D. 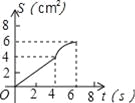
 A
【解析】试题分析:分两种情况:①当0≤t<4时,作OG⊥AB于G,如图1所示,由正方形的性质得出∠B=90°,AD=AB=BC=4cm,AG=BG=OG=AB=2cm,由三角形的面积得出S=AP•OG=t();②当t≥4时,作OG⊥AB于G,如图2所示,S=△OAG的面积+梯形OGBP的面积=×2×2+(2+t﹣4)×2=t();综上所述:面积S()与时间t(s)的关系的图象是过原点的线...
A
【解析】试题分析:分两种情况:①当0≤t<4时,作OG⊥AB于G,如图1所示,由正方形的性质得出∠B=90°,AD=AB=BC=4cm,AG=BG=OG=AB=2cm,由三角形的面积得出S=AP•OG=t();②当t≥4时,作OG⊥AB于G,如图2所示,S=△OAG的面积+梯形OGBP的面积=×2×2+(2+t﹣4)×2=t();综上所述:面积S()与时间t(s)的关系的图象是过原点的线... 如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是_____.
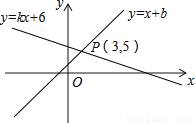
 x>3.
【解析】试题解析:当x>3时,x+b>kx+6,
即不等式x+b>kx+6的解集为x>3.
x>3.
【解析】试题解析:当x>3时,x+b>kx+6,
即不等式x+b>kx+6的解集为x>3. 下列结论中,正确的是( )
A. 若a>b,则 <
<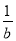 B. 若a>b,则a2>b2
B. 若a>b,则a2>b2
C. 若a>b,则1-a<1-b D. 若a>b,ac2>bc2
 C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C.
C
【解析】当1>a>b>0时, <,故不正确;当a>0,b<0,a<|b|时,a2<b2,故不正确;由a>b可知-a<-b,因此可得1-a<1-b,故正确;当c=0时,虽然a>b,但是ac2=bc2=0,故不正确.
故选:C. 在□ABCD中,∠A+∠C=270°,则∠B=______,∠C=______.
 45° 135°
【解析】【解析】
∵已知平行四边形ABCD,∴∠A=∠C,∠B+∠C=180°.
又∵∠A+∠C=270°,∴2∠C=270°,∠C=135°,∴∠B=180°-∠C=180°-135°=45°.
故答案为:∠C=135°,∠B=45°.
45° 135°
【解析】【解析】
∵已知平行四边形ABCD,∴∠A=∠C,∠B+∠C=180°.
又∵∠A+∠C=270°,∴2∠C=270°,∠C=135°,∴∠B=180°-∠C=180°-135°=45°.
故答案为:∠C=135°,∠B=45°. 在□ABCD中,对角线AC,BD相交于O点,AC=10,BD=8,则AD长的取值范围是 ( )
A. AD>1 B. AD<9 C. 1<AD<9 D. AD>10
 C
【解析】【解析】
平行四边形的对角线互相平分得:两条对角线的一半分别是5,4.再根据三角形的三边关系,得:1<AD<9.故选C.
C
【解析】【解析】
平行四边形的对角线互相平分得:两条对角线的一半分别是5,4.再根据三角形的三边关系,得:1<AD<9.故选C. BD是□ABCD的对角线,点E,F在BD上,要使四边形AECF是平行四边形,还需添加的条件是______(只添一个你认为正确的即可).
 BE=DF等
【解析】【解析】
如图,连接AC交BD于点O.
∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,∴可增加BE=DF.故答案为:BE=DF(答案不唯一).
BE=DF等
【解析】【解析】
如图,连接AC交BD于点O.
∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形,∴可增加BE=DF.故答案为:BE=DF(答案不唯一). 已知多边形内角和与外角和的和为2160°,求多边形对角线的条数.
 54
【解析】分析:已知一个多边形的内角和与外角和的差为2160°,外角和是360度,因而内角和是1800度.n边形的内角和是(n-2) ×180°,代入就得到一个关于n的方程,就可以解得边数n,从而得到这个多边形的对角线的条数.
本题解析:
设这是n边形,则
(n-2)×180°=2160°-360°,
n-2=10,
n=12.
这个多边形的对角线的条数=12×(12...
54
【解析】分析:已知一个多边形的内角和与外角和的差为2160°,外角和是360度,因而内角和是1800度.n边形的内角和是(n-2) ×180°,代入就得到一个关于n的方程,就可以解得边数n,从而得到这个多边形的对角线的条数.
本题解析:
设这是n边形,则
(n-2)×180°=2160°-360°,
n-2=10,
n=12.
这个多边形的对角线的条数=12×(12... 
