题目内容
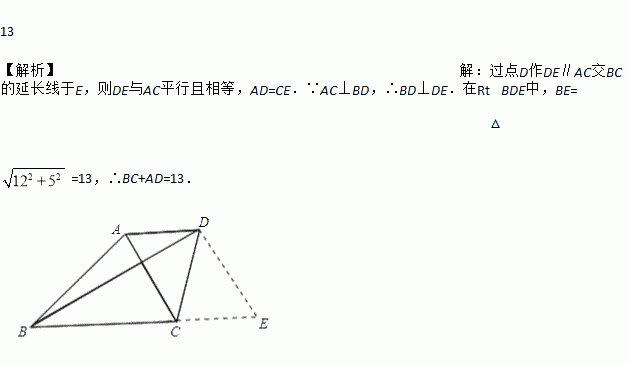
如图所示，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC＝5 ㎝， BD＝12 ㎝，则该梯形的两底之和等于____㎝．
13
【解析】【解析】
过点D作DE∥AC交BC的延长线于E，则DE与AC平行且相等，AD=CE．∵AC⊥BD，∴BD⊥DE．在Rt△BDE中，BE==13，∴BC+AD=13．
练习册系列答案
相关题目
已知a,b,c为△ABC三边长,且满足a2c2－b2c2=a4－b4，则它的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形
D
【解析】试题分析：由a2c2-b2c2=a4-b4，得
a4+b2c2-a2c2-b4=（a4-b4）+（b2c2-a2c2）=（a2+b2）（a2-b2）-c2（a2-b2）=（a2-b2）（a2+b2-c2）=（a+b）（a-b）（a2+b2-c2）=0，
∵a+b＞0，∴a-b=0或a2+b2-c2=0，
即a=b或a2+b2=c2，则△ABC为等腰三角形或直角三... 二次函数y=ax2＋bx﹣1（a≠0）的图象经过点（1，1），则a＋b＋1的值是
A. ﹣3 B. ﹣1 C. 2 D. 3
D
【解析】试题分析：根据二次函数图象上点的坐标特征，把（1，1）代入解析式可得到a+b﹣1=1，则a+b=2，所以a+b+1=3.
故选：D． 不等式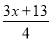
＞
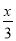＋2的解是_________.
x＞－3
【解析】＞＋2, 去分母得： 去括号得： 移项及合并得： 系数化为1得： .
故答案为x＞－3. 如图所示，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝24 ㎝，BC＝26㎝，动点P从点A开始沿AD边以每秒1㎝的速度向D点运动，动点Q从点C开始沿CB边以每秒3㎝的速度向B运动，P，Q分别从A，C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t s．
（1）t为何值时，四边形PQCD为平行四边形?
（2）t为何值时，四边形PQCD为等腰梯形?
（3）t为何值时，四边形ABQP为矩形?
（1）t＝6时；（2）t＝7时；（3）t＝时.
【解析】试题分析：（1）要使四边形PQCD是平行四边形，则点在运动的过程中，只需PD=QC就满足题意；
（2）作DE⊥BC，PF⊥BC，垂足分别为E，F，要使四边形PQCD为等腰梯形，则QF＝CE；依此即可求解；
（3）要使四边形ABQP为矩形，则点在运动的过程中，只需AP=BQ就满足题意．
试题解析：【解析】
由已知得AP... 在□ABCD中，AB=3，BC=4，则□ABCD的周长等于_______.
14
【解析】【解析】
∵四边形ABCD是平行四边形，∴CD=AB=3，AD=BC=4，∴?ABCD的周长为14．
故答案为：14． □ABCD的周长为36 cm，AB=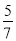
BC，则较长边的长为（ ）
A. 15 cm B. 7.5 cm C. 21 cm D. 10.5 cm
D
【解析】【解析】
∵?ABCD的周长=2（AB+BC）=36，∴AB+BC=18．∵AB=BC，∴BC=10.5．
故选D． 四边形ABCD中，AD//BC，AD＝BC，则四边形ABCD是_______四边形．
平行
【解析】【解析】
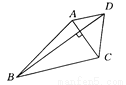
∵AD//BC，AD＝BC，∴四边形ABCD是平行四边形．故答案为：平行． （10分） 如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．
360°．
【解析】试题分析：连接BE，根据三角形外角的性质可得∠1=∠C+∠D=∠CBE+∠DEB，再由四边形的内角和定理可得∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F=360°．
试题解析：【解析】
如图，连接BE．
∵∠1=∠C+∠D，∠1=∠CBE+∠DEB，
∴∠C+∠D=∠CB...