题目内容
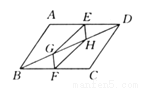
如图所示，E，F分别为平行四边形ABCD中AD，BC的中点，G，H在BD上，且 BG＝DH，求证四边形EGFH是平行四边形．
答案见解析
【解析】试题分析：由四边形ABCD是平行四边形，得到AD=BC，AD∥BC，由AD∥BC，得到∠ADB=∠DBC，因为E、F分别为?ABCD的边AD、BC的中点，得到DE=BF，由三角形全等证得EH=FG，∠EHD=∠FGB，得到EH∥FG，证出四边形FGEH是平行四边形．
试题解析：证明：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠ADB=∠DBC．∵E、...
练习册系列答案
相关题目
分解因式：4x2－9y2.
(2x＋3y)(2x－3y)
【解析】试题分析：直接利用平方差公式因式分解即可.
试题解析：
4x2－9y2=(2x＋3y)(2x－3y). 二次函数y＝x2－4x－3的顶点坐标是_____________．
（2,﹣7）
【解析】试题分析：原式化为顶点式解析式，即为y=(x-2)2-7,所以其顶点坐标是（2,﹣7）． 任取不等式组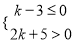
的一个整数解，则能使关于x的方程：2x＋k＝－1的解为非负数的可能性为____.
【解析】解不等式k-3≤0可得k≤3，解不等式2k+5＞0，可得k＞-，所以可求得不等式组的解集为-＜k≤3，所以k的整数解为-2、-1、0、1、2、3，分别代入方程2x+k=-1，可得x=、0、-、-1、-、-2，所以非负数解有了两个，其可能性为： .
故答案为： . 不等式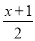
＞
－1的正整数解的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
D
【解析】根据不等式的解法，去分母，得3（x+1）＞2（2x+2）-6，去括号得3x+3＞4x+4-6，移项合并同类项，x＜5，可得其正整数解为1、2、3、4，共4个.
故选：D. 和直线l距离为8 cm的直线有______条.
2
【解析】【解析】
在同一平面上，和直线l距离为8cm的直线在直线L的两侧各有一条．故答案为：2． 下列不能作为判定四边形ABCD为平行四边形的条件的是（ ）
A. AB＝CD，AD＝BC B. AB
CD
C. AB＝CD，AD∥BC D. AB∥CD，AD∥BC
C
【解析】解：A．∵AB=CD，AD=BC，∴四边形ABCD的两组对边相等，可以判定四边形ABCD是平行四边形；故本选项不合题意；
B．∵AB∥CD，AB=CD，∴四边形ABCD的一组对边平行且相等，可以判定四边形ABCD是平行四边形；故本选项不合题意；
C．∵AB=CD，AD∥CD，无法判定四边形ABCD是平行四边形；故本选项合题意；
D．∵AB∥CD，AD∥BC，四边... M是△ABC的AB边上的中点，连接CM并延长到D，使MD＝CM，则AD与BC________，BD与AC________。
平行且相等 平行且相等
【解析】【解析】
如图，∵M是△ABC的AB边上的中点，∴AM=MB．∵MD＝CM，∴四边形ADBC是平行四边形，∴AD=CB，AD∥CB，BD=AC，BD∥AC．故答案为：平行且相等，平行且相等． 在四边形ABCD中，∠A＝∠C＝90°，∠B与∠D的度数比是3：2，求∠B，∠D的度数．
∠B＝108°，∠D＝72°．
【解析】分析：由已知∠A=∠C=90°,较易得到∠B+∠D=180°,再根据已知的∠B:∠D=3:2,即可求解.
本题解析：
∵∠ A ＋∠ C ＝90°＋90°＝180°，∴∠ B ＋∠ D ＝360°－(∠ A ＋∠ C )＝360°－1 80°＝180°．设∠ B ＝( 3 x )°，则∠ D ＝(2 x )°，∴(3 x )°＋(2 x )...