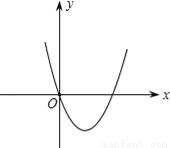
如图所示是二次函数y=ax2﹣x+a2﹣1的图象,则a的值是( )
A. a=﹣1 B. a= C. a=1 D. a=1或a=﹣1
C. a=1 D. a=1或a=﹣1
 C
【解析】由图象得,此二次函数过原点(0,0),
把点(0,0)代入函数解析式得a2-1=0,解得a=±1;
又因为此二次函数的开口向上,所以a>0;
所以a=1.
故选C.
C
【解析】由图象得,此二次函数过原点(0,0),
把点(0,0)代入函数解析式得a2-1=0,解得a=±1;
又因为此二次函数的开口向上,所以a>0;
所以a=1.
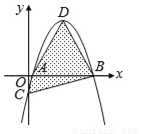
故选C. 如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
A. 1 B. 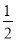 C.
C. 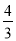 D.
D. 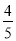
 D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D.
D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D. 在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 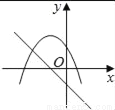 B.
B. 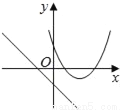 C.
C. 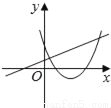 D.
D. 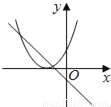
 D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=?mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<...
D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=?mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<... 如图所示的抛物线是二次函数y= +bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b,其中正确的结论有( ).
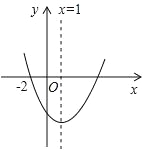
A.1个 B.2个 C.3个 D.4个
 C.
【解析】
试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C...
C.
【解析】
试题分析:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x==1,∴b=﹣2a<0,所以②正确;∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc>0,所以①正确;∵点(﹣2,0)关于直线x=1的对称点的坐标为(4,0),∴抛物线与x轴的另一个交点坐标为(4,0),所以③正确;∵x=﹣1时,y<0,
即a﹣b+c<0,∴a+c<b,所以④错误.
故选:C... 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )

A. -1<x<4 B. -1<x<3 C. x<-1或x>4 D. x<-1或x>3
 B
【解析】由图象知,抛物线与x轴交于(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∵y<0时,函数的图象位于x轴的下方,
且当-1<x<3时函数图象位于x轴的下方,
∴当-1<x<3时,y<0.
故选B.
B
【解析】由图象知,抛物线与x轴交于(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∵y<0时,函数的图象位于x轴的下方,
且当-1<x<3时函数图象位于x轴的下方,
∴当-1<x<3时,y<0.
故选B. 如图,小姚身高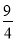 m在某次投篮中,球的运动路线是抛物线
m在某次投篮中,球的运动路线是抛物线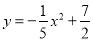 的一部分,若命中篮圈中心,则他与篮底的距离
的一部分,若命中篮圈中心,则他与篮底的距离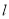 是( )
是( )
A. 3.5m B. 4m C. 4.5m D. 4.6m
 B
【解析】试题分析:分别求出当y=3.05和当y=时的x的值,前面那个取正数,后面的那个取负数,然后计算它们之间的距离.
B
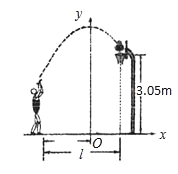
【解析】试题分析:分别求出当y=3.05和当y=时的x的值,前面那个取正数,后面的那个取负数,然后计算它们之间的距离. 二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( )
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
 C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C.
C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C. 已知抛物线的解析式为y=(x-2)2+1,则这条抛物线的顶点坐标是( ).
A. (﹣2,1) B. (2,1) C. (2,﹣1) D. (1,2)
 B
【解析】根据顶点式y=(x-h)2+k的顶点为(h,k),由y=(x-2)2+1为抛物线的顶点式,顶点坐标为(2,1).
故选:B.
B
【解析】根据顶点式y=(x-h)2+k的顶点为(h,k),由y=(x-2)2+1为抛物线的顶点式,顶点坐标为(2,1).
故选:B. 已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为( )
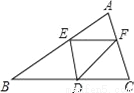
A. 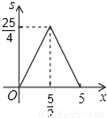 B.
B. 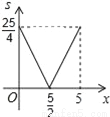 C.
C. 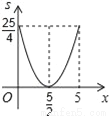 D.
D. 
 D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
故选D.
D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
故选D. 如果函数y=(k-3) +kx+1是二次函数,那么k的值一定是 .
+kx+1是二次函数,那么k的值一定是 .
 0.
【解析】试题解析:由题意得:k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
0.
【解析】试题解析:由题意得:k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.