题目内容
二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）
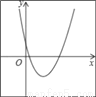
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
C
【解析】试题分析：根据抛物线的顶点在第四象限，得出n＜0，m＜0，即可得出一次函数y=mx+n的图象经过二、三、四象限．
故选C．
抛物线y=x2﹣2x﹣3的图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=x2+bx+c，则b、c的值为（ ）
A．b=2，c=2 B．b=2，c=﹣1 C．b=﹣2，c=﹣1 D．b=﹣3，c=2
B．
【解析】
试题分析：y=x2﹣2x﹣3=x2﹣2x+1﹣4=（x﹣1）2﹣4，
图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=（x﹣1+2）2﹣4+2=（x+1）2﹣2=x2+2x﹣1，
则b=2，c=﹣1，
故选B． 下列长度的各组线段中，能组成三角形的是 ( )
A. 4、5、6 B. 6、8、15 C. 5、7、12 D. 3、9、13
A
【解析】根据三角形的三边关系，得
A.4+5>6，能组成三角形，符合题意；
B.6+8<15，不能够组成三角形，不符合题意；
C.5+7=12，不能够组成三角形，不符合题意；
D.3+7<13，不能够组成三角形，不符合题意。
故选：A. 广东特产专卖店销售龙眼干，其进价为每斤40元，按每斤60元出售，平均每天可售出100斤，后来经调查发现，单价每降低2元，则平均每天的销售量增加20斤．每斤降价多少元，每天销售额最大？
20元
【解析】
试题分析：根据题意可以列出销售额与销售单价之间的关系式，然后整理为顶点式，即可解答本题．
【解析】
设每斤降价x元，销售额为y元，
y=（60﹣x）（100+）=﹣10（x﹣25）2+12250，
∴当x＜25时，y随x的增大而增大，
∵60﹣40=20，
∴0≤x≤20，
∴当x=20时，y取得最大值，
即每斤降价20元时... 某工厂有一种产品现在的年产量是20万件，计划今后两年增加产量，如果每年都比上一年的产量增加x倍，那么两年后这种产品的产量y将随计划所定的x的值而确定，那么y与x之间的关系应表示为_____．
y=20(x+1)2
【解析】∵某工厂一种产品的年产量是20件，每一年都比上一年的产品增加x倍，
∴一年后产品是：20（1+x），
∴两年后产品y与x的函数关系是：y=20（1+x）2．
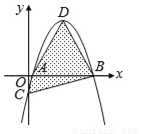
故答案为：y=20（x+1）2. 如图，坐标平面上，二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点，与y轴交于C点，其顶点为D，且k＞0．若△ABC与△ABD的面积比为1：4，则k值为何？（ ）
A. 1 B.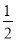 
C. 
D. 
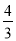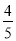
D
【解析】试题分析：∵y=﹣x2+4x﹣k=﹣（x﹣2）2+4﹣k，∴顶点D（2，4﹣k），C（0，﹣k），∴OC=k，∵△ABC的面积=AB•OC=AB•k，△ABD的面积=AB（4﹣k），△ABC与△ABD的面积比为1：4，∴k=（4﹣k），解得：k=．故选D． 如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at2＋5t＋c，已知足球飞行0.8s时，离地面的高度为3.5m.
(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？
(2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x＝10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？
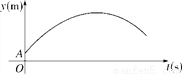
（1）足球飞行的时间是s时，足球离地面最高，最大高度是4.5m；（2）能.
【解析】试题分析：（1）由题意得：函数y=at2+5t+c的图象经过（0，0.5）（0.8，3.5），于是得到，求得抛物线的解析式为：y=﹣t2+5t+，当t=时，y最大=4.5；
（2）把x=28代入x=10t得t=2.8，当t=2.8时，y=﹣×2.82+5×2.8+=2.25＜2.44，于是得到他能将球直... 抛物线y=﹣（x+2）2﹣3的顶点坐标是（ ）
A. （2，﹣3） B. （﹣2，3） C. （2，3） D. （﹣2，﹣3）
D
【解析】试题分析：∵抛物线y=﹣（x+2）2﹣3为抛物线解析式的顶点式，∴抛物线顶点坐标是（﹣2，﹣3）．故选D． 如图所示，AD为△ABC的一条角平分线，E，F分别在AC，AB上，DE∥AB，BF＝AE．试说明EF＝BD．
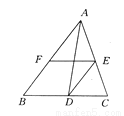
答案见解析
【解析】试题分析：由角平分线的定义和平行线的性质可证明∠ADE=∠CAD，可得AE=DE，结合条件可证明四边形EFBD为平行四边形，可得EF=BD．
试题解析：证明：∵AD平分∠BAC，∴∠BAD=∠CAD．∵DE∥AB，∴∠BAD=∠ADE，∴∠CAD=∠ADE，∴AE=DE．又∵BF=AE，∴DE=BF．又∵DE∥AB，∴四边形EFBD是平行四边形，∴EF=BD．
...