题目内容
如图，小姚身高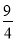
m在某次投篮中，球的运动路线是抛物线
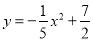的一部分，若命中篮圈中心，则他与篮底的距离
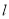是（ ）
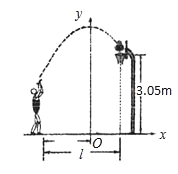
A. 3.5m B. 4m C. 4.5m D. 4.6m
B
【解析】试题分析：分别求出当y=3.05和当y=时的x的值，前面那个取正数，后面的那个取负数，然后计算它们之间的距离.
名校课堂系列答案如图所示是二次函数y=ax2﹣x+a2﹣1的图象，则a的值是（ ）
A. a=﹣1 B. a=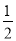
C. a=1 D. a=1或a=﹣1
C
【解析】由图象得，此二次函数过原点（0，0），
把点（0，0）代入函数解析式得a2-1=0，解得a=±1；
又因为此二次函数的开口向上，所以a＞0；
所以a=1．
故选C． 一个钝角三角形的三条角平分线所在的直线一定交于一点，这交点一定在( )
A. 三角形内部 B. 三角形的一边上 C. 三角形外部 D. 三角形的某个顶点上
A
【解析】三角形三条角平分线所在的直线一定交于一点，这一点是三角形的内心即内切圆的圆心，此点在三角形（锐角三角形、直角三角形、钝角三角形）内部.
故选：A. 二次函数y=ax2+bx+c的图象过A（﹣3，0），B（1，0），C（0，3），点D在函数图象上，点C，D是二次函数图象上的一对对称点，一次函数图象过点B，D，求：
（1）一次函数和二次函数的解析式；
（2）写出使一次函数值大于二次函数值的x的取值范围．
（1）y1=﹣x2﹣2x+3（2）x＜﹣2或x＞1．
【解析】
试题分析：（1）将A、B、C的坐标代入抛物线的解析式中即可求得二次函数的解析式，进而可根据抛物线的对称轴求出D点的坐标，再用待定系数法求出一次函数解析式；
（2）根据（1）画出函数图象，即可写出一次函数值大于二次函数值的x的取值范围．
【解析】
（1）二次函数y1=ax2+bx+c的图象经过点A（﹣3，0），... 已知抛物线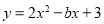
的对称轴是直线
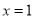，则
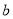的值为 ．
b=4
【解析】
试题分析：由抛物线的对称轴x=-和已知条件抛物线y=2-bx+3的对称轴是直线x=1，得到的等式，即可求出b的值． 如图所示是二次函数y=ax2﹣x+a2﹣1的图象，则a的值是（ ）
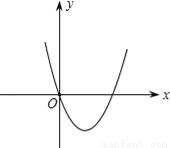
A. a=﹣1 B. a=
C. a=1 D. a=1或a=﹣1
C
【解析】由图象得，此二次函数过原点（0，0），
把点（0，0）代入函数解析式得a2-1=0，解得a=±1；
又因为此二次函数的开口向上，所以a＞0；
所以a=1．
故选C． 已知抛物线y=ax2+bx+3的对称轴是直线x=1．
（1）求证：2a+b=0；
（2）若关于x的方程ax2+bx﹣8=0的一个根为4，求方程的另一个根．
（1）见解析；（2）x=－2
【解析】试题分析：直接利用对称轴公式代入求出即可；根据（1）中所求，再将x=4代入方程求出a，b的值，进而解方程得出即可．
试题解析：（1）证明：∵对称轴是直线x=1=﹣，∴b=－2a ∴2a+b=0；
（2）∵ax2+bx﹣8=0的一个根为4，∴16a+4b﹣8=0，∵b=﹣2a，∴16a﹣8a﹣8=0，
解得：a=1，则b=﹣2，∴a+bx... （2016四川省泸州市）某商店购买60件A商品和30件B商品共用了1080元，购买50件A商品和20件B商品共用了880元．
（1）A、B两种商品的单价分别是多少元？
（2）已知该商店购买B商品的件数比购买A商品的件数的2倍少4件，如果需要购买A、B两种商品的总件数不少于32件，且该商店购买的A、B两种商品的总费用不超过296元，那么该商店有哪几种购买方案？
（1）A种商品的单价为16元、B种商品的单价为4元；（2）有两种方案：方案（1）：m=12，2m﹣4=20 即购买A商品的件数为12件，则购买B商品的件数为20件；方案（2）：m=13，2m﹣4=22 即购买A商品的件数为13件，则购买B商品的件数为22件．
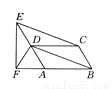
【解析】试题分析：(1)、设A种商品的单价为x元、B种商品的单价为y元，根据题意得出方程组，从而求出x和y的值；(2)、设购买A商品的... 如图所示，在
ABCD中，CE∥BD，EF⊥AB交BA延长线于点F，E，D，A在一条直线上，那么有DF＝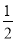
AE，请你说明理由．(提示：直角三角形中斜边中线等于斜边的一半)
答案见解析
【解析】试题分析：首先根据平行四边形的性质可得AD=BC，AD∥BC，再证明四边形EDBC是平行四边形，可得ED=CB，然后根据直角三角形斜边上的中线等于斜边的一半可得结论．
试题解析：证明：∵四边形ABCD为平行四边形，∴AD=BC，AD∥BC．∵CE∥BD，∴四边形EDBC是平行四边形，∴ED=CB，∴ED=AD．∵EF⊥AB，∴△EFA是直角三角形，∴DF=AE．