题目内容
如果函数y=(k-3) +kx+1是二次函数,那么k的值一定是 .
+kx+1是二次函数,那么k的值一定是 .
 0.
【解析】试题解析:由题意得:k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
0.
【解析】试题解析:由题意得:k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
练习册系列答案
相关题目
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
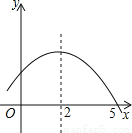
A. -1<x<5 B. x>5 C. x<-1且x>5 D. x<-1或x>5
 D
【解析】由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点坐标为(5,0),
∴函数图象与x轴的另一交点坐标为(-1,0),
∴ax2+bx+c<0的解集是x<-1或x>5.
故选C.
D
【解析】由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点坐标为(5,0),
∴函数图象与x轴的另一交点坐标为(-1,0),
∴ax2+bx+c<0的解集是x<-1或x>5.
故选C. 等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是( )
A. x<6 B. 6<x<12 C. 0<x<12 D. x>12
 B
【解析】等腰三角形的周长为24cm,腰长为xcm,则底边长为24-2x,
根据三边关系,x+x>24-2x,解得,x>6;
x-x<24-2x,解得,x<12,
所x的取值范围是6<x<12.
故选:C.
B
【解析】等腰三角形的周长为24cm,腰长为xcm,则底边长为24-2x,
根据三边关系,x+x>24-2x,解得,x>6;
x-x<24-2x,解得,x<12,
所x的取值范围是6<x<12.
故选:C. 下列各式中,能用平方差公式因式分解的是( )
A. x2+x B. x2+8x+16 C. x2+4 D. x2﹣1
 D
【解析】A. x²+x=x(x+1),是提取公因式法分解因式,故此选项错误;
B. x²+8x+16=(x+4)²,是公式法分解因式,故此选项错误;
C. x²+4,无法分解因式,故此选项错误;
D. x²?1=(x+1)(x?1),能用平方差公因式分解,故此选项正确。
故选:D.
D
【解析】A. x²+x=x(x+1),是提取公因式法分解因式,故此选项错误;
B. x²+8x+16=(x+4)²,是公式法分解因式,故此选项错误;
C. x²+4,无法分解因式,故此选项错误;
D. x²?1=(x+1)(x?1),能用平方差公因式分解,故此选项正确。
故选:D. 如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线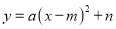 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。
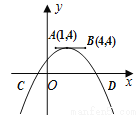
 8
【解析】当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小,把A(1,4)代入得:y=a(x-1)2+4,把C(-3,0)代入得:0=a(-3-1)2+4,解得:a=-,即:y=-(x-1)2+4,再根据题意知抛物线y=a(x-m)2+n的顶点在线段AB上运动,可得抛物线的a永远等于-,当抛物线的顶点运动到B时,D的横坐标最大,把a=-和B(4,4)代入y=a(x...
8
【解析】当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小,把A(1,4)代入得:y=a(x-1)2+4,把C(-3,0)代入得:0=a(-3-1)2+4,解得:a=-,即:y=-(x-1)2+4,再根据题意知抛物线y=a(x-m)2+n的顶点在线段AB上运动,可得抛物线的a永远等于-,当抛物线的顶点运动到B时,D的横坐标最大,把a=-和B(4,4)代入y=a(x... 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )

A. -1<x<4 B. -1<x<3 C. x<-1或x>4 D. x<-1或x>3
 B
【解析】由图象知,抛物线与x轴交于(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∵y<0时,函数的图象位于x轴的下方,
且当-1<x<3时函数图象位于x轴的下方,
∴当-1<x<3时,y<0.
故选B.
B
【解析】由图象知,抛物线与x轴交于(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∵y<0时,函数的图象位于x轴的下方,
且当-1<x<3时函数图象位于x轴的下方,
∴当-1<x<3时,y<0.
故选B. 已知二次函数y=2x2+bx﹣1.
(1)求证:无论b取什么值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点.
(2)若两点P(﹣3,m)和Q(1,m)在该函数图象上.
①求b、m的值;
②将二次函数图象向上平移多少单位长度后,得到的函数图象与x轴只有一个公共点?
 (1)无论b取什么值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点.
(2)b=4,m=5;(3)二次函数图象向上平移3个单位
【解析】
试题分析:(1)先计算判别式的值,再利用非负数的性质可判断△=>0,然后根据判别式的意义可判断抛物线与x轴必有两个交点;
(2)①先利用抛物线的对称性可确定抛物线的对称轴方程,从而可求出b的值,然后计算自变量为1所对应的函数值即可得...
(1)无论b取什么值,二次函数y=2x2+bx﹣1图象与x轴必有两个交点.
(2)b=4,m=5;(3)二次函数图象向上平移3个单位
【解析】
试题分析:(1)先计算判别式的值,再利用非负数的性质可判断△=>0,然后根据判别式的意义可判断抛物线与x轴必有两个交点;
(2)①先利用抛物线的对称性可确定抛物线的对称轴方程,从而可求出b的值,然后计算自变量为1所对应的函数值即可得... 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 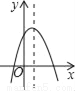 B.
B. 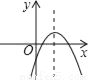 C.
C. 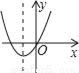 D.
D. 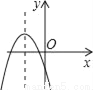
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
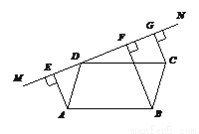
故选B. 如图,直线MN过□ABCD的顶点D,过A,B,C三点,分别作MN的垂线,垂足分别是E,F,G.
求证:DE=FG.
 答案见解析
【解析】试题分析:作CH⊥BF与H.可证△AED≌△BHC,得到ED=HC,再由平行线间的距离处处相等得到FG=CH,即可得到结论.
试题解析:证明:作CH⊥BF与H.
∵AE⊥MN,BF⊥MN,∴AE∥BF,∴∠EAD+∠DAB+∠ABF=180°.
∵ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠DAB+∠ABF+∠HBC=180°,∴∠EAD=∠HB...
答案见解析
【解析】试题分析:作CH⊥BF与H.可证△AED≌△BHC,得到ED=HC,再由平行线间的距离处处相等得到FG=CH,即可得到结论.
试题解析:证明:作CH⊥BF与H.
∵AE⊥MN,BF⊥MN,∴AE∥BF,∴∠EAD+∠DAB+∠ABF=180°.
∵ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠DAB+∠ABF+∠HBC=180°,∴∠EAD=∠HB... 
