题目内容
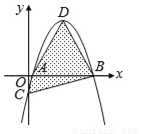
如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
A. 1 B. 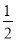 C.
C. 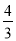 D.
D. 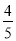
 D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D.
D
【解析】试题分析:∵y=﹣x2+4x﹣k=﹣(x﹣2)2+4﹣k,∴顶点D(2,4﹣k),C(0,﹣k),∴OC=k,∵△ABC的面积=AB•OC=AB•k,△ABD的面积=AB(4﹣k),△ABC与△ABD的面积比为1:4,∴k=(4﹣k),解得:k=.故选D.
二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( )
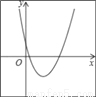
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
 C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C.
C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C. 分解因式:16(x-y)2-9(x+y)2.
 (7x-y)(x-7y)
【解析】试题分析:利用平方差公式因式分解即可.
试题解析:
16(x-y)2-9(x+y)2
=[4(x-y)-3(x+y)][4(x-y)+3(x+y)]
=(x-7y)(7x-y).
(7x-y)(x-7y)
【解析】试题分析:利用平方差公式因式分解即可.
试题解析:
16(x-y)2-9(x+y)2
=[4(x-y)-3(x+y)][4(x-y)+3(x+y)]
=(x-7y)(7x-y). 将抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位,那么得到的抛物线的表达式为 .
 y=2﹣2
【解析】试题分析:按照“左加右减,上加下减”的规律可得抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位得到y=2(x﹣1+3)2+2﹣4=2(x+2)2﹣2.即可得抛物线的解析式为y=2(x+2)2﹣2.
y=2﹣2
【解析】试题分析:按照“左加右减,上加下减”的规律可得抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位得到y=2(x﹣1+3)2+2﹣4=2(x+2)2﹣2.即可得抛物线的解析式为y=2(x+2)2﹣2. 二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( )
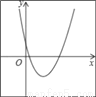
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
 C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C.
C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C. 如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.
探究1:如果木板边长为1米,FC=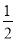 米,则一块木板用墙纸的费用需 元;
米,则一块木板用墙纸的费用需 元;
探究2:如果木板边长为2米,正方形EFCG的边长为x米,一块木板需用墙纸的费用为y元,

(1)用含x的代数式表示y(写过程).
(2)如果一块木板需用墙纸的费用为225元,求正方形EFCG的边长为多少米?
 (1)55,y=20x2﹣40x+240(2)正方形EFCG的边长为或米
【解析】【解析】
探究1:∵四边形ABCD是正方形,
∴AB=BC=CD=DA=1,
∴S正方形ABCD=1,
∵四边形EFCG是正方形,
∴EF=CF=,
∴S正方形EFCG=,BF=,
∴S△ABE==
∴空白部分的面积为:1﹣﹣=,
∴这块木板用墙纸的费用为:+8...
(1)55,y=20x2﹣40x+240(2)正方形EFCG的边长为或米
【解析】【解析】
探究1:∵四边形ABCD是正方形,
∴AB=BC=CD=DA=1,
∴S正方形ABCD=1,
∵四边形EFCG是正方形,
∴EF=CF=,
∴S正方形EFCG=,BF=,
∴S△ABE==
∴空白部分的面积为:1﹣﹣=,
∴这块木板用墙纸的费用为:+8... 如图在平面直角坐标系中,二次函数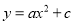 的图象过正方形ABOC的三个顶点A、B、C,则
的图象过正方形ABOC的三个顶点A、B、C,则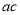 值为__________。
值为__________。
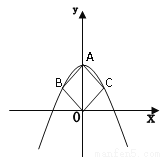
 -2
【解析】试题解析:设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:
c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=-,
则ac=-•2m=-2.
-2
【解析】试题解析:设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:
c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=-,
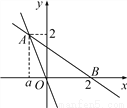
则ac=-•2m=-2. 如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.
 (1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:【解析】
(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)...
(1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:【解析】
(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)... 一个四边形的边长依次是a,b,c,d,且a2+b2+c2+d2=2ac+2bd,则这个四边形是______,依据是________.
 平行四边形 两组对边分别相等的四边形是平行四边形
【解析】【解析】
a2+b2+c2+d2=2ac+2bd,(a2﹣2ac+c2)+(b2﹣2bd+d2)=0,(a﹣c)2+(b﹣d)2=0,∴a﹣c=0,b﹣d=0,∴a=c,b=d,∴四边形是平行四边形(两组对边分别相等的四边形是平行四边形).故答案为:平行四边形,两组对边分别相等的四边形是平行四边形.
平行四边形 两组对边分别相等的四边形是平行四边形
【解析】【解析】
a2+b2+c2+d2=2ac+2bd,(a2﹣2ac+c2)+(b2﹣2bd+d2)=0,(a﹣c)2+(b﹣d)2=0,∴a﹣c=0,b﹣d=0,∴a=c,b=d,∴四边形是平行四边形(两组对边分别相等的四边形是平行四边形).故答案为:平行四边形,两组对边分别相等的四边形是平行四边形. 
