题目内容
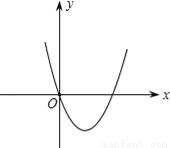
如图所示是二次函数y=ax2﹣x+a2﹣1的图象，则a的值是（ ）
A. a=﹣1 B. a=
C. a=1 D. a=1或a=﹣1
C
【解析】由图象得，此二次函数过原点（0，0），
把点（0，0）代入函数解析式得a2-1=0，解得a=±1；
又因为此二次函数的开口向上，所以a＞0；
所以a=1．
故选C．
练习册系列答案
小学课时特训系列答案
相关题目
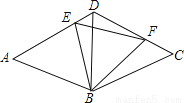
如图，等边三角形ABD和等边三角形CBD的边长均为a，现把它们拼合起来，E是AD上异于A、D两点的一动点，F是CD上一动点，满足AE+CF=a．则△BEF的形状如何？
△BEF为正三角形，理由见解析
【解析】试题分析：根据已知条件易证△BDE≌△BCF，即可求得∠FBD+∠DBE=60°，根据一个内角为60°的等腰三角形可以判定为等边三角形，即可得结论．
试题解析：
△BEF为正三角形
证明：∵AE+CF=a，AE+ED=a，
∴DE=CF，
在△BDE和△BCF中，
∴△BDE≌△BCF，
∴BE=BF，∠CBF... 分解因式：4m3n－16mn3.
4mn(m＋2n)(m－2n)
【解析】试题分析：提取公因式4mn后，再利用平方差公式因式分解即可.
试题解析：
4m3n－16mn3
=4mn(m2－4n2)
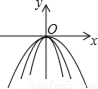
=4mn(m＋2n)(m－2n). 如图所示，在同一平面直角坐标系中，作出①y=﹣3x2，②y=﹣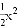
，③y=﹣x2的图象，则从里到外的三条抛物线对应的函数依次是______（填序号）
① ③ ②
【解析】①y=?3x²，②y=?x²，③y=?x²中,二次项系数a分别为?3、?、?1，
∵|?3|>|?1|>，∴抛物线②y=?x²的开口最宽,抛物线①y=?3x²的开口最窄。
故答案为：①③②。 如图，小姚身高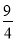
m在某次投篮中，球的运动路线是抛物线
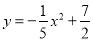的一部分，若命中篮圈中心，则他与篮底的距离
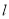是（ ）
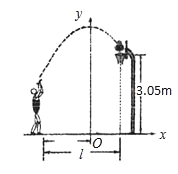
A. 3.5m B. 4m C. 4.5m D. 4.6m
B
【解析】试题分析：分别求出当y=3.05和当y=时的x的值，前面那个取正数，后面的那个取负数，然后计算它们之间的距离. 已知二次函数的图象经过点（0，﹣3），且顶点坐标为（﹣1，﹣4）．
（1）求该二次函数的解析式；
（2）设该二次函数的图象与x轴的交点为A、B，与y轴的交点为C，求△ABC的面积．
1.【解析】
（1）设，把点代入得：-----------2分
∴函数解析式或-----------------------------2分
2.（2）∵，解得，
∴，，。---------（2分）
∴△ABC的面积=。--------------------------（2分）
【解析】试题分析：（1）先设所求函数解析式是y=a（x+1）2﹣4，再把（0，﹣3）代... 已知点P（-1，m）在二次函数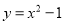
的图象上，则m的值为____________；
0
【解析】∵点P（-1，m）在二次函数y=x2-1的图象上，
∴m=1-1=0．
故答案是：0． (1)解不等式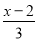
－
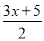≥x－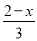
，并把它的解集在数轴上表示出来．
(2)解不等式组： 
，并把解集在数轴上表示出来．
（1）x≤－1，解集在数轴上表示见解析；（2）原不等式组无解.
【解析】试题分析：（1）根据不等式的解法，利用去分母，去括号，移项合并同类项，系数化为1，解不等式，再表示在数轴上即可；
（2）分别解两个不等式，然后求出不等式组的解集，并表示在数轴上.
试题解析：(1) 【解析】
原不等式化简为：2x－4－9x－15≥6x－4＋2x，解得x≤－1，解集在数轴上表示为：
(2... 如图所示，已知AD∥BC，要使四边形ABCD为平行四边形，需要增加的条件是________．(只需填一个你认为正确的条件即可).
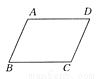
AD＝BC，或AB∥AD(答案不唯一)
【解析】【解析】
根据平行四边形的判定方法，需要增加的条件是：AD=BC或AB∥CD或∠A=∠C或∠B=∠D．故答案为：AD=BC（或AB∥CD）．