如图,等边三角形ABD和等边三角形CBD的边长均为a,现把它们拼合起来,E是AD上异于A、D两点的一动点,F是CD上一动点,满足AE+CF=a.则△BEF的形状如何?
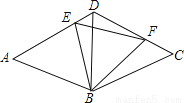
 △BEF为正三角形,理由见解析
【解析】试题分析:根据已知条件易证△BDE≌△BCF,即可求得∠FBD+∠DBE=60°,根据一个内角为60°的等腰三角形可以判定为等边三角形,即可得结论.
试题解析:
△BEF为正三角形
证明:∵AE+CF=a,AE+ED=a,
∴DE=CF,
在△BDE和△BCF中,
∴△BDE≌△BCF,
∴BE=BF,∠CBF...
△BEF为正三角形,理由见解析
【解析】试题分析:根据已知条件易证△BDE≌△BCF,即可求得∠FBD+∠DBE=60°,根据一个内角为60°的等腰三角形可以判定为等边三角形,即可得结论.
试题解析:
△BEF为正三角形
证明:∵AE+CF=a,AE+ED=a,
∴DE=CF,
在△BDE和△BCF中,
∴△BDE≌△BCF,
∴BE=BF,∠CBF... 二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( )
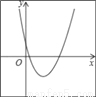
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
 C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C.
C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C. 函数y=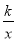 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A. 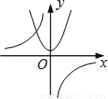 B.
B. 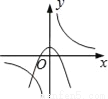 C.
C. 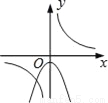 D.
D. 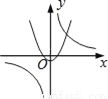
 B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
...
B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
... 关于二次函数y=x2﹣2x﹣3的图象,下列说法中错误的是( )
A. 当x<2,y随x的增大而减小 B. 函数的对称轴是直线x=1
C. 函数的开口方向向上 D. 函数图象与y轴的交点坐标是(0,﹣3)
 A
【解析】试题分析:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线开口向上,对称轴为x=1,当x<1时y随x的增大而减小,故B、C正确,A不正确,
令x=0可得y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),故D正确,
故选A.
A
【解析】试题分析:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线开口向上,对称轴为x=1,当x<1时y随x的增大而减小,故B、C正确,A不正确,
令x=0可得y=﹣3,
∴抛物线与y轴的交点坐标为(0,﹣3),故D正确,
故选A. 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 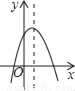 B.
B. 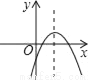 C.
C. 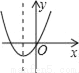 D.
D. 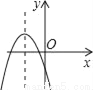
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B. 如图所示是二次函数y=ax2﹣x+a2﹣1的图象,则a的值是( )

A. a=﹣1 B. a=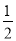 C. a=1 D. a=1或a=﹣1
C. a=1 D. a=1或a=﹣1
 C
【解析】由图象得,此二次函数过原点(0,0),
把点(0,0)代入函数解析式得a2-1=0,解得a=±1;
又因为此二次函数的开口向上,所以a>0;
所以a=1.
故选C.
C
【解析】由图象得,此二次函数过原点(0,0),
把点(0,0)代入函数解析式得a2-1=0,解得a=±1;
又因为此二次函数的开口向上,所以a>0;
所以a=1.
故选C. 抛物线y=x2﹣2x﹣3的图象向左平移2个单位,再向上平移2个单位,所得图象的解析式为y=x2+bx+c,则b、c的值为( )
A.b=2,c=2 B.b=2,c=﹣1 C.b=﹣2,c=﹣1 D.b=﹣3,c=2
 B.
【解析】
试题分析:y=x2﹣2x﹣3=x2﹣2x+1﹣4=(x﹣1)2﹣4,
图象向左平移2个单位,再向上平移2个单位,所得图象的解析式为y=(x﹣1+2)2﹣4+2=(x+1)2﹣2=x2+2x﹣1,
则b=2,c=﹣1,
故选B.
B.
【解析】
试题分析:y=x2﹣2x﹣3=x2﹣2x+1﹣4=(x﹣1)2﹣4,
图象向左平移2个单位,再向上平移2个单位,所得图象的解析式为y=(x﹣1+2)2﹣4+2=(x+1)2﹣2=x2+2x﹣1,
则b=2,c=﹣1,
故选B. 根据下列表格对应值:
x | 3 | 4 | 5 |
y=ax2+bx+c | 0.5 | ﹣0.5 | ﹣1 |
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
A. x<3 B. x>5 C. 3<x<4 D. 4<x<5
 C
【解析】试题分析:∵x=3时,y=0.5,即ax2+bx+c>0;
x=4时,y=﹣0.5,即ax2+bx+c<0,
∴抛物线与x轴的一个交点在(3,0)和(4,0)之间,
∴关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是3<x<4.
故选C.
C
【解析】试题分析:∵x=3时,y=0.5,即ax2+bx+c>0;
x=4时,y=﹣0.5,即ax2+bx+c<0,
∴抛物线与x轴的一个交点在(3,0)和(4,0)之间,
∴关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是3<x<4.
故选C. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
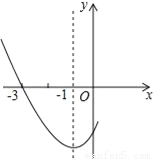
A. ①② B. ②③ C. ①②④ D. ②③④
 A
【解析】∵抛物线开口向上,∴a>0,∵抛物线对称轴为直线x=﹣=﹣1,∴b=2a>0,则2a﹣b=0,所以②正确;
∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc<0,所以①正确;
∵x=2时,y>0,∴4a+2b+c>0,所以③错误;
∵点(﹣5,y1)离对称轴的距离与点(3,y2)离对称轴的距离相等,∴y1=y2,所以④不正确.
故选:A.
A
【解析】∵抛物线开口向上,∴a>0,∵抛物线对称轴为直线x=﹣=﹣1,∴b=2a>0,则2a﹣b=0,所以②正确;
∵抛物线与y轴的交点在x轴下方,∴c<0,∴abc<0,所以①正确;
∵x=2时,y>0,∴4a+2b+c>0,所以③错误;
∵点(﹣5,y1)离对称轴的距离与点(3,y2)离对称轴的距离相等,∴y1=y2,所以④不正确.
故选:A. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
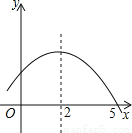
A. -1<x<5 B. x>5 C. x<-1且x>5 D. x<-1或x>5
 D
【解析】由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点坐标为(5,0),
∴函数图象与x轴的另一交点坐标为(-1,0),
∴ax2+bx+c<0的解集是x<-1或x>5.
故选C.
D
【解析】由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点坐标为(5,0),
∴函数图象与x轴的另一交点坐标为(-1,0),
∴ax2+bx+c<0的解集是x<-1或x>5.
故选C.