题目内容
关于二次函数y=x2﹣2x﹣3的图象，下列说法中错误的是（ ）
A. 当x＜2，y随x的增大而减小 B. 函数的对称轴是直线x=1
C. 函数的开口方向向上 D. 函数图象与y轴的交点坐标是（0，﹣3）
A
【解析】试题分析：∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴抛物线开口向上，对称轴为x=1，当x＜1时y随x的增大而减小，故B、C正确，A不正确，
令x=0可得y=﹣3，
∴抛物线与y轴的交点坐标为（0，﹣3），故D正确，
故选A．
阅读快车系列答案袋中有5个红球，6个白球，12个黑球，每个球除颜色外都相同，事先选定一种颜色，若摸到的球的颜色与事先选定的一样，则获胜，否则就失败，为了尽可能获胜，你事先应选择的颜色是__．
黑色
【解析】先分别求出摸到红球，白球，黑球的概率，再比较它们的大小，概率最大的即为所求．
【解析】
∵袋中有5个红球，6个白球，12个黑球，
∴袋中一共有球：5+6+12=23（个），
∴摸到红球的概率为： ，
摸到白球的概率为： ，
摸到黑球的概率为： ，
又∵＜＜，
∴摸到黑球的概率最大，会尽可能获胜．
故答案为黑球． 在平面直角坐标系中，线段OP的两个端点坐标分别为O（0，0），P（4， 3），将线段OP绕点O逆时针旋转90°到OP′位置，则点P′的坐标是（ ）
A．（3，4） B．（－4，3） C．（－3，4） D．（4，－3）
C．
【解析】
试题分析：如图，OA=3，PA=4，
把线段OP绕点O逆时针旋转90°到OP′位置可得OA旋转到x轴负半轴OA′的位置，OB旋转到y轴正半轴OB′的位置,所以P′A′=PA=4，P′B′=PB=3,即可得P′点的坐标为（﹣3，4）．故答案选C． 二次函数y=x2+bx+c的图象经过点（4，3），（3，0）．
（1）求b、c的值；
（2）求该二次函数图象的顶点坐标和对称轴．
（1） ；（2）顶点坐标为（2，﹣1），对称轴为直线x=2
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式.
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴ ，
解得 ；
（2）∵该二次函数为y=x2﹣4x+3=（x... 如图是二次函数y=ax2+bx+c图象的一部分，其对称轴是x=﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（ ）
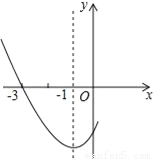
A. ①② B. ②③ C. ①②④ D. ②③④
A
【解析】∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；
∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；
∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；
∵点（﹣5，y1）离对称轴的距离与点（3，y2）离对称轴的距离相等，∴y1=y2，所以④不正确．
故选：A． 如图，在△ABC中，AB=AC，BF=CD，BD=CE，∠FDE=α，探索α与∠B的关系。
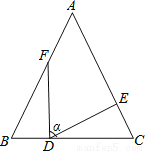
∠α=∠B，理由见解析
【解析】试题分析：根据已知条件易证△BFD≌△CDE，得出∠BFD=∠CDE，再由角之间的转化，进而可得出结论．
【解析过程】
试题解析：
∠α=∠B，理由为：
证明：∵AB=AC（已知），
∴∠B=∠C（等边对等角），
在△BDF和△CED中，
∴△BDF≌△CED（SAS），
∴∠BFD=∠CDE（全等三角形对应角相... 若等腰三角形有两条边的长度为2和5，则此等腰三角形的周长为（ ）
A. 9 B. 12 C. 9或12 D. 10
B
【解析】由于等腰三角形的底边不确定，所以需要分类讨论，
①当底边长为2时，三边长为2，5，5，则周长为2+5+5=12；
②当底边长为5时，三边长为5，2，2，但5＞2+2，不能构成三角形.
故选B. 如果△ABC中，两边a＝7cm，b＝3cm，则c的取值范围是_________；第三边为奇数的所有可能值为_________；周长为偶数的所有可能值为_________．
4cm＜c＜10cm 5cm、7cm、9cm 16cm或18cm
【解析】根据三角形的三边关系，得7cm?3cm如图所示的抛物线是二次函数y=
+bx+c（a≠0）的图象，则下列结论：①abc＞0；②b+2a=0；③抛物线与x轴的另一个交点为（4，0）；④a+c＞b，其中正确的结论有（ ）.
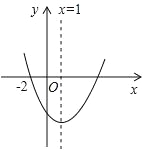
A．1个 B．2个 C．3个 D．4个
C．
【解析】
试题分析：∵抛物线开口向上，∴a＞0，∵抛物线的对称轴为直线x==1，∴b=﹣2a＜0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＞0，所以①正确；∵点（﹣2，0）关于直线x=1的对称点的坐标为（4，0），∴抛物线与x轴的另一个交点坐标为（4，0），所以③正确；∵x=﹣1时，y＜0，
即a﹣b+c＜0，∴a+c＜b，所以④错误．
故选：C...