题目内容
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
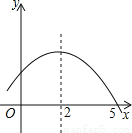
A. -1<x<5 B. x>5 C. x<-1且x>5 D. x<-1或x>5
 D
【解析】由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点坐标为(5,0),
∴函数图象与x轴的另一交点坐标为(-1,0),
∴ax2+bx+c<0的解集是x<-1或x>5.
故选C.
D
【解析】由图可知,抛物线的对称轴为直线x=2,与x轴的一个交点坐标为(5,0),
∴函数图象与x轴的另一交点坐标为(-1,0),
∴ax2+bx+c<0的解集是x<-1或x>5.
故选C.
练习册系列答案
相关题目
从1,2,3,4,5这五个数中任意取两个相乘,问:
(1)积为偶数,属于哪类事件?有几种可能情况?
(2)积为奇数,属于哪类事件?有几种可能情况?
(3)积为无理数,属于哪类事件?
 (1)可能事件,7;(2)可能事件,3;(3)不可能事件
【解析】试题分析:(1),(2)由于五个数中任意取两数相乘有奇数有偶数,所以(1)(2)都为不确定事件,分别写出乘积为偶数与为奇数的情况,即可看出分别有几种情况.
(3)由于五个数都是有理数,他们的乘积也一定为有理数,不可能为无理数,所以(3)为不可能事件.
试题解析: 取任意两个数相乘,可能的结果如下表所示(重复的不留在表中...
(1)可能事件,7;(2)可能事件,3;(3)不可能事件
【解析】试题分析:(1),(2)由于五个数中任意取两数相乘有奇数有偶数,所以(1)(2)都为不确定事件,分别写出乘积为偶数与为奇数的情况,即可看出分别有几种情况.
(3)由于五个数都是有理数,他们的乘积也一定为有理数,不可能为无理数,所以(3)为不可能事件.
试题解析: 取任意两个数相乘,可能的结果如下表所示(重复的不留在表中... 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________度.
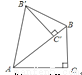
 20°
【解析】试题分析:根据旋转图形可得∠B′AB=40°,AB=AB′,则∠B′BA=70°,根据∠BCB′=90°可得∠BB′C=90°-70°=20°.
20°
【解析】试题分析:根据旋转图形可得∠B′AB=40°,AB=AB′,则∠B′BA=70°,根据∠BCB′=90°可得∠BB′C=90°-70°=20°. 如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(﹣2,0),
B(4,0)与y轴交于点C.
(Ⅰ)求抛物线的解析式及其顶点D的坐标;
(Ⅱ)求△BCD的面积;
(Ⅲ)若直线CD交x轴与点E,过点B作x轴的垂线,交直线CD与点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究抛物线最多可以向上平移多少个单位长度(直接写出结果,不写求解过程).
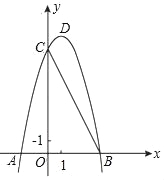
 (Ⅰ)抛物线的解析式:y=﹣x2+2x+8=﹣(x﹣1)2+9,顶点D(1,9);(Ⅱ)6;(Ⅲ)72.
【解析】
试题分析:(Ⅰ)利用待定系数法求出抛物线的解析式,通过对解析式进行配方能得到顶点D的坐标;
(Ⅱ)先求出直线BC解析式,进而用三角形的面积公式即可得出结论.
(Ⅲ)首先确定直线CD的解析式以及点E,F的坐标,若抛物线向上平移,首先表示出平移后的函数解析式;当x...
(Ⅰ)抛物线的解析式:y=﹣x2+2x+8=﹣(x﹣1)2+9,顶点D(1,9);(Ⅱ)6;(Ⅲ)72.
【解析】
试题分析:(Ⅰ)利用待定系数法求出抛物线的解析式,通过对解析式进行配方能得到顶点D的坐标;
(Ⅱ)先求出直线BC解析式,进而用三角形的面积公式即可得出结论.
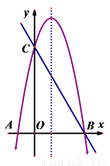
(Ⅲ)首先确定直线CD的解析式以及点E,F的坐标,若抛物线向上平移,首先表示出平移后的函数解析式;当x... 如图,抛物线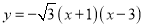 与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
 或
【解析】试题分析:如图所示:
∵抛物线y=﹣(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,
∴当﹣(x+1)(x﹣3)=0时,x=﹣1,或x=3,
当x=0时,y=3,
∴A(﹣1,0),B(3,0),C(0,3),对称轴x=1,
∴BM=3﹣1=2,
当点D到直线BC和到x轴的距离相等时,点D在∠ABC或∠ABE的平分线上,
①点D...
或
【解析】试题分析:如图所示:
∵抛物线y=﹣(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,
∴当﹣(x+1)(x﹣3)=0时,x=﹣1,或x=3,
当x=0时,y=3,
∴A(﹣1,0),B(3,0),C(0,3),对称轴x=1,
∴BM=3﹣1=2,
当点D到直线BC和到x轴的距离相等时,点D在∠ABC或∠ABE的平分线上,
①点D... 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 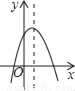 B.
B. 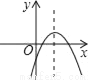 C.
C. 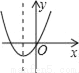 D.
D. 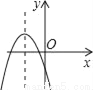
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B. 如图,已知△ABC中,AB=AC,周长为24,AC边上的中线BD把△ABC分成周长差为6的两个三角形,则△ABC各边的长分别为多少?
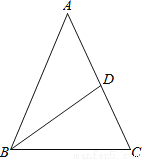
 三角形的各边长为10、10、4
【解析】试题分析:分AB>BC和AB<BC两种情况求得AB、BC的长,再由三角形的三边关系进行取舍即可.
试题解析:
根据题意结合图形,分成两部分的周长的差等于腰长与底边的差,
(1)若AB>BC,则AB-BC=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=10,BC=4,
10、10、4三边能够组成三角形;
...
三角形的各边长为10、10、4
【解析】试题分析:分AB>BC和AB<BC两种情况求得AB、BC的长,再由三角形的三边关系进行取舍即可.
试题解析:
根据题意结合图形,分成两部分的周长的差等于腰长与底边的差,
(1)若AB>BC,则AB-BC=6,
又因为2AB+BC=24,
联立方程组并求解得:AB=10,BC=4,
10、10、4三边能够组成三角形;
... △ABC中,AB=5,BC=3,则中线BD的取值范围是_________.
 1<BD<4
【解析】延长BD到E,使BD=DE,连接AE,如图:
∵BD是△ABC中线,
∴AD=DC,
在△BDC和△EDA中,
∵,
∴△BDC≌△EDA.
∴BC=AE=3,
∵在△ABE中,根据三角形的三边关系定理得:5+3>BE>5-3,
∴2<2BD<8,
即1<BD<4.
故答案为:1<BD<4.
1<BD<4
【解析】延长BD到E,使BD=DE,连接AE,如图:
∵BD是△ABC中线,
∴AD=DC,
在△BDC和△EDA中,
∵,
∴△BDC≌△EDA.
∴BC=AE=3,
∵在△ABE中,根据三角形的三边关系定理得:5+3>BE>5-3,
∴2<2BD<8,
即1<BD<4.
故答案为:1<BD<4. 如果函数y=(k-3) +kx+1是二次函数,那么k的值一定是 .
+kx+1是二次函数,那么k的值一定是 .
 0.
【解析】试题解析:由题意得:k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
0.
【解析】试题解析:由题意得:k2-3k+2=2,
解得k=0或k=3;
又∵k-3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数. 
