题目内容
如图所示是二次函数y=ax2﹣x+a2﹣1的图象，则a的值是（ ）
A. a=﹣1 B. a=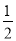
C. a=1 D. a=1或a=﹣1
C
【解析】由图象得，此二次函数过原点（0，0），
把点（0，0）代入函数解析式得a2-1=0，解得a=±1；
又因为此二次函数的开口向上，所以a＞0；
所以a=1．
故选C．
名校课堂系列答案玉树地震灾区小朋友卓玛从某地捐赠的2种不同款式的书包和2种不同款式的文具盒中，分别取一个书包和一个文具盒进行款式搭配，则不同搭配的可能有__种．
4
【解析】【解析】
每种书包有2种不同款式的文具盒搭配，2种书包就有2×2=4种搭配方式 关于这一图案，下列说法正确的是（ ）
A. 图案乙是由甲绕BC的中点旋转180°得到的
B. 图案乙是由甲绕点C旋转108°得到的
C. 图案乙是由甲沿AB方向平移3个边长的距离得到的
D. 图案乙是由甲沿直线BC翻转180°得到的
A
【解析】【解析】
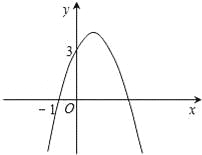
如图所示：可得图案乙是由甲绕BC的中点旋转180°得到的．故选A． 已知二次函数y=﹣x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（﹣1，0），与y轴的交点坐标为（0，3）．
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，写出函数值y为正数时，自变量x的取值范围．
（1）b="2,c=3," y=﹣x2+2x+3．(2) ﹣1＜x＜3
【解析】试题分析：（1）把抛物线上的两点代入解析式，解方程组可求b、c的值；
（2）令y=0，求抛物线与x轴的两交点坐标，观察图象，求y＞0时，x的取值范围．
试题解析：（1）将点（﹣1，0），（0，3）代入y=﹣x2+bx+c中，得
，解得．
∴y=﹣x2+2x+3．
（2）令y=0，解方... 已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1）、P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且﹣1＜x1＜x2，x3＜﹣1，则y1、y2、y3的大小关系为（ ）
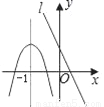
A. y1＜y2＜y3 B. y3＜y1＜y2 C. y3＜y2＜y1 D. y2＜y1＜y3
D
【解析】解析：对称轴为直线x=﹣1，且﹣1＜x1＜x2，当x＞﹣1时，y2＜y1，
又因为x3＜﹣1，由一次函数的图象可知，此时点P3（x3，y3）在二次函数图象上方，
所以y2＜y1＜y3．
故选：D． 如图，等边三角形ABD和等边三角形CBD的边长均为a，现把它们拼合起来，E是AD上异于A、D两点的一动点，F是CD上一动点，满足AE+CF=a．则△BEF的形状如何？
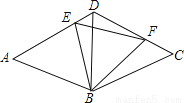
△BEF为正三角形，理由见解析
【解析】试题分析：根据已知条件易证△BDE≌△BCF，即可求得∠FBD+∠DBE=60°，根据一个内角为60°的等腰三角形可以判定为等边三角形，即可得结论．
试题解析：
△BEF为正三角形
证明：∵AE+CF=a，AE+ED=a，
∴DE=CF，
在△BDE和△BCF中，
∴△BDE≌△BCF，
∴BE=BF，∠CBF... 如图，已知DE∥BC，AB=AC，∠1=125°，则∠C的度数是（ ）
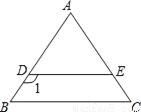
A. 55° B. 45° C. 35° D. 65°
A
【解析】∵∠1=125°，DE∥BC，∴∠B=180°–125°=55°，∵AB=AC，∴∠C=∠B=55°，故选A． 过△ABC的顶点C作边AB的垂线将∠ACB分为20°和40°的两个角，那么∠A，∠B中较大的角的度数是____________．
70°
【解析】根据题意画出图形，则∠ACD=40°，∠DCB=20°.
∵CD⊥AB，∠ACD=40°，∠DCB=20°，
∴∠A=50°，∠B=70°，
∴∠A、∠B中较大的角的度数是70°.
故答案为：70°. 如图，小姚身高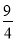
m在某次投篮中，球的运动路线是抛物线
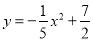的一部分，若命中篮圈中心，则他与篮底的距离
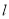是（ ）
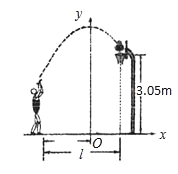
A. 3.5m B. 4m C. 4.5m D. 4.6m
B
【解析】试题分析：分别求出当y=3.05和当y=时的x的值，前面那个取正数，后面的那个取负数，然后计算它们之间的距离.