题目内容
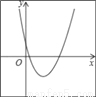
二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
C
【解析】试题分析：根据抛物线的顶点在第四象限，得出n＜0，m＜0，即可得出一次函数y=mx+n的图象经过二、三、四象限．
故选C．
练习册系列答案
阅读快车系列答案
相关题目
下列事件中，是必然事件的是（ ）
A. 打开电视机，里面正在转播足球比赛 B. 小麦的亩产量一定为1000公斤
C. 在只装有5个红球的袋中摸出1球是红球 D. 在农历十五的晚上，一定能看到圆月
C
【解析】选项A，B，D选项为不确定事件，即随机事件；选项C是必然发生事件．故选C． 如图，若△DEF是由△ABC经过平移后得到的，则平移的距离是（ ）
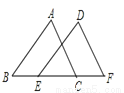
A. 线段BC的长度 B. 线段BE的长度 C. 线段EC的长度 D. 线段EF的长度
B
【解析】试题分析：对应点之间的距离就是平移的距离，根据题意可得：点B和点E对应，则线段BE的长度就是平移的距离. 若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是__．
0或1
【解析】需要分类讨论：①若m=0，则函数为一次函数；②若m≠0，则函数为二次函数，由抛物线与x轴只有一个交点，得到根的判别式的值等于0，且m不为0，即可求出m的值．
【解析】
①若m=0，则函数y=2x+1，是一次函数，与x轴只有一个交点；
②若m≠0，则函数y=mx2+2x+1，是二次函数．
根据题意得：△=4﹣4m=0，
解得：m=1．
所以当m的... 抛物线y=x2﹣2x﹣3的图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=x2+bx+c，则b、c的值为（ ）
A．b=2，c=2 B．b=2，c=﹣1 C．b=﹣2，c=﹣1 D．b=﹣3，c=2
B．
【解析】
试题分析：y=x2﹣2x﹣3=x2﹣2x+1﹣4=（x﹣1）2﹣4，
图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y=（x﹣1+2）2﹣4+2=（x+1）2﹣2=x2+2x﹣1，
则b=2，c=﹣1，
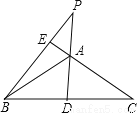
故选B． 如图，在等腰三角形ABC中，AD、BE分别是底边BC和腰AC上的高线，DA、BE的延长线交于点P．若∠BAC=110°，求∠P的度数。
35°
【解析】试题分析：根据等腰三角形三线合一的性质可求得∠DAC的度数，根据对顶角相等求得∠EAP的度数，再由直角三角形的两锐角互余即可求得∠P的度数.
试题解析：
∵△ABC是等腰三角形，AB=AC，AD⊥BC，∠BAC=110°，
∴∠DAB=∠DAC=55°，
∵∠DAC=∠EAP（对顶角相等），
∴∠EAP=∠DAC=55°，
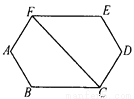
又∵BE是腰AC... 已知：如图，AB＝DE，CD＝FA，∠A＝∠D，∠AFC＝∠DCF，则BC＝EF．你能说出它们相等的理由吗?
见解析
【解析】试题分析：首先连接CE、BF，然后根据条件可证明△ABF≌△DEC，再根据全等三角形的性质可得∠3=∠4，BF=EC，然后证明△BCF≌△EFC可得BC=EF．
试题解析：连接CE、BF，如图：
在△ABF和△DEC中， ，
∴△ABF≌△DEC(SAS)，
∴∠3=∠4，BF=EC，
∵∠AFC=∠DCF，
∴∠AFC?∠3=∠DCF?∠... 如图，直线
、
、
表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有( )
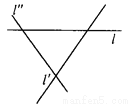
A. 一处 B. 二处 C. 三处 D. 四处
D
【解析】如图所示，加油站站的地址有四处.
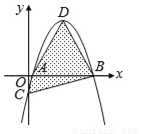
故选：D. 如图，坐标平面上，二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点，与y轴交于C点，其顶点为D，且k＞0．若△ABC与△ABD的面积比为1：4，则k值为何？（ ）
A. 1 B.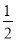 
C. 
D. 
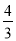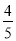
D
【解析】试题分析：∵y=﹣x2+4x﹣k=﹣（x﹣2）2+4﹣k，∴顶点D（2，4﹣k），C（0，﹣k），∴OC=k，∵△ABC的面积=AB•OC=AB•k，△ABD的面积=AB（4﹣k），△ABC与△ABD的面积比为1：4，∴k=（4﹣k），解得：k=．故选D．