如图，已知AB=AD给出下列条件：
（1）CB=CD （2）∠BAC=∠DAC （3）∠BCA=∠DCA （4）∠B=∠D，
若再添一个条件后，能使△ABC≌△ADC的共有（ ）
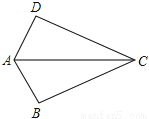
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】∵在△ABC和△ADC中，AB=AD，AC=AC，
∴（1）添加“CB=CD”可由“SSS”判定△ABC≌△ADC；
（2）添加“∠BAC=∠DAC”可由“SAS”判定△ABC≌△ADC；
（3）添加“∠BCA=∠DCA”不能判定△ABC≌△ADC；
（4）添加“∠B=∠D”不能判定△ABC≌△ADC；
即4个条件中，添加（1）和（2）能使△ABC≌... 如图，已知AB∥CD，AE=CF，则下列条件中不一定能使△ABE≌△CDF的是（ ）
A. AB=CD B. BE∥DF C. ∠B=∠D D. BE=DF
D
【解析】∵AB∥CD，
∴∠A=∠C，
又∵AE=CF，
∴（1）添加“AB=CD”，可由“SAS”判定△ABE≌△CDF；
（2）添加“BE∥DF”可得∠FEB=∠EFD，进一步可得∠AEB=∠CFD，从而可由“ASA”判定△ABE≌△CDF；
（3）添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF；
（4）添加“BE=DF”不能判定△ABE≌... 如图，已知AC与BD相交于点O，OA=OC，OB=OD，则图中有多少对三角形全等（ ）
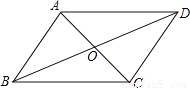
A. 1 B. 2 C. 3 D. 4
D
【解析】∵AC与BD相交于点O，
∴∠AOD=∠COB，∠AOB=∠COD，
又∵OA=OC，OB=OD，
∴△AOD≌△COB，△AOB≌△COD，
∴AD=CB，AB=CD，
又∵AC=CA，BD=DB，
∴△ACD≌△CAB，△ABD≌△CDB，
即图中共有4对全等三角形.
故选D. 如图，下列条件能保证△ABC≌△ADC的是：①AB=AD，BC=DC；②∠1=∠3，∠4=∠2；③∠1=∠2，∠4=∠3；④∠1=∠2，AB=AD；⑤∠1=∠2，BC=DC．（ ）
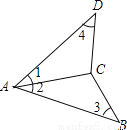
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
C
【解析】∵在△ABC和△ADC中，AC=AC，
∴当添加条件：①AB=AD，BC=DC时，可由“SSS”得到△ABC≌△ADC；
当添加条件：②∠1=∠3，∠4=∠2时，不能得到△ABC≌△ADC；
当添加条件：③∠1=∠2，∠4=∠3时，可由“AAS”得到△ABC≌△ADC；
当添加条件：④∠1=∠2，AB=AD时，可由“SAS”得到△ABC≌△ADC；
... 如图，△ABC和△AED中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD、CE，求证：BD=EC。
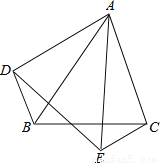
证明见解析
【解析】试题分析：
由∠BAC=∠DAE易得∠BAD=∠EAC，结合AB=AE，AC=AD，即可由“SAS”证得：△BAD≌△EAC，从而可得：BD=EC.
试题解析：
∵∠DAE=∠BAC，
∴∠DAE-∠BAE=∠EAC-∠BAE，
∴∠BAD=∠EAC，
在△BAD和△EAC中，
∴△BAD≌△EAC（SAS），
∴BD=EC... 如图，BE、CF是△ABC的高且相交于点P，AQ∥BC交CF延长线于点Q，若有BP=AC，CQ=AB，线段AP与AQ的关系如何？说明理由。
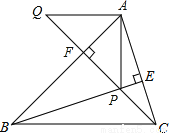
证明见解析
【解析】试题分析：
由BE、CF是△ABC的高，易得∠ABP+∠BPF=90°，∠ACP+∠CPE=90°，结合∠BPF=∠CPE，易得∠ABP=∠ACP，这样结合BP=AC，CQ=AB，即可由“SAS”证得△ACQ≌△PBA，从而可得AP=AQ，∠Q=∠PAF，结合∠PAF+∠APF=90°，可得：∠APF+∠Q=90°，即可得到∠QAP=90°，从而可得AQ⊥AP，由此... 如图，△ABC中，∠ACB=90°，CD⊥AB于点D，AO平分∠BAC，交CD于点O，E为AB上一点，且AE=AC。
（1）求证：△AOC≌△A0E；
（2）求证：OE∥BC。
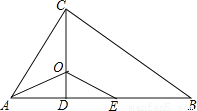
（1）证明见解析（2）证明见解析
【解析】试题分析：
（1）由AO平分∠BAC，可得∠CAO=∠EAO结合AO=AO，AE=AC即可由“SAS”证得：△AOC≌△AOE；
（2）由△AOC≌△AOE可得∠ACO=∠AEO，由∠ACB=90°，CD⊥AB于点D，易得∠ACO+∠DCB=90°，∠AEO+∠EOD=90°，从而可得∠DCB=∠DOE，即可得到：OE∥BC.
试题... 如图1，四边形ABCD中，AD∥BC，∠ABC=∠DCB，AB=DC。
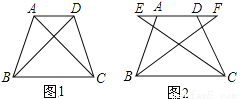
（1）求证：AC=DB；
（2）如图2，E、F两点同时从A、D出发在直线AD上以相同的速度反向而行，BF和CE会相等吗？请证明你的结论。
（1）证明见解析（2）BF=CE
【解析】试题分析：
（1）由∠ABC=∠DCB，AB=DC结合BC=CB即可证得：△ABC≌△DCB，从而可得AC=DB；
（2）由题意可得AE=DF，从而可得AF=DE，由AD∥BC结合∠ABC=∠DCB，易得∠BAD=∠CDA，再结合AB=DC即可证得△BAF≌△CDE，从而可得BF=CE.
试题解析：
（1）在△ABC和△DCB... 如图，点B、D、E、C在一条直线上，△ABD≌△ACE，AB和AC，AD和AE是对应边，除△ABD≌△ACE外，图中还有其他全等三角形吗？若有，请写出来，并证明你的结论。
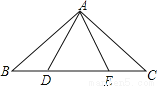
有，△ABE≌△ACD
【解析】试题分析：
由△ABD≌△ACE可得：AB=AC，BD=CE，∠B=∠C，从而易得BE=CD，这样由“SAS”即可证得△ABE和△ACD.
试题解析：
有，△ABE≌△ACD；理由如下：
∵△ABD≌△ACE，
∴AB=AC，BD=CE，∠B=∠C，
∴BE=CD，
在△ABE和△ACD中，
，
∴△ABE... 如图，在△ABC和△DEC中，∠ABC=∠DEC=90°，连接AD交射线EB于F，AC∥DE，延长CA交射线EB于点G，点F恰好是AD中点。
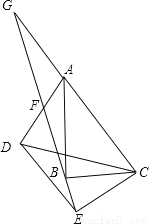
（1）求证：△AFG≌△DFE；
（2）若BC=CE，
①求证：∠ABF=∠DEF；
②若∠BAC=30°，试求∠AFG的度数。
（1）证明见解析（2）①证明见解析②∠AFG=60°。
【解析】试题分析：
（1）由AG∥DE易得：∠G=∠DEF；由F是AD的中点易得AF=DF，结合∠AFG=∠DFE，即可证得：△AGF≌△DEF；
（2）①由BC=CE可得∠CBE=∠CEB，结合∠ABC=DEC=90°，易得∠ABF+∠CBE=90°，∠CEB+∠DEF=90°，从而可得∠ABF=∠DEF；
②由△A...