题目内容
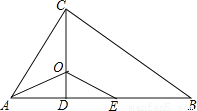
如图，△ABC中，∠ACB=90°，CD⊥AB于点D，AO平分∠BAC，交CD于点O，E为AB上一点，且AE=AC。
（1）求证：△AOC≌△A0E；
（2）求证：OE∥BC。
（1）证明见解析（2）证明见解析
【解析】试题分析：
（1）由AO平分∠BAC，可得∠CAO=∠EAO结合AO=AO，AE=AC即可由“SAS”证得：△AOC≌△AOE；
（2）由△AOC≌△AOE可得∠ACO=∠AEO，由∠ACB=90°，CD⊥AB于点D，易得∠ACO+∠DCB=90°，∠AEO+∠EOD=90°，从而可得∠DCB=∠DOE，即可得到：OE∥BC.
试题...
练习册系列答案
相关题目
若代数式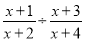
有意义，则x的取值范围是________
，
【解析】试题解析：因为x+2≠0，且x+4≠0，所以x≠?2且x≠?4.
又0作除数无意义，所以x+3≠0，即x≠?3.
故空中填：x≠?2，?3，?4.
故答案为： ， 且. 计算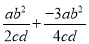 
的结果是（ ）
A. 
B. 
C. 
D. －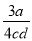
C
【解析】试题分析：原式＝＋
＝
＝．
故选C． x取什么值时，代数式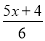
的值不小于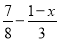
的值？并求x的最小值．
x≥－，最小值为－.
【解析】【试题分析】根据题意，列出不等式 ，求出不等式的解集x≥－即可.
【试题解析】
由题意得：
，
去分母得： ，
去括号得：
移项得：
合并同类项得： 系数化为1得： .
x的最小值为－.
故答案为x≥－，最小值为－. 若
x2m－1－8＞5是一元一次不等式，则m的值为( )
A. 0 B. 1
C. 2 D. 3
B
【解析】根据一元一次不等式的定义得： ，故选B. 如图，已知AB∥CD，AE=CF，则下列条件中不一定能使△ABE≌△CDF的是（ ）
A. AB=CD B. BE∥DF C. ∠B=∠D D. BE=DF
D
【解析】∵AB∥CD，
∴∠A=∠C，
又∵AE=CF，
∴（1）添加“AB=CD”，可由“SAS”判定△ABE≌△CDF；
（2）添加“BE∥DF”可得∠FEB=∠EFD，进一步可得∠AEB=∠CFD，从而可由“ASA”判定△ABE≌△CDF；
（3）添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF；
（4）添加“BE=DF”不能判定△ABE≌... 甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费，设小红在同一商场累计购物x元，其中x＞100．
（1）根据题意，填写下表（单位：元）；
累计购物 实际花费 | 130 | 290 | … | x |
在甲商场 | 127 |
| … |
|
在乙商场 | 126 |
| … |
|
（2）当x取何值时，小红在甲、乙两商场的实际花费相同？
（3）当小红在同一商场累计购物超过100元时，在哪家商场的实际花费少？
（1）在甲商场：100+（290﹣100）×0.9=271，100+（x﹣100）×0.9=0.9x+10；
在乙商场：50+（290﹣50）×0.95=278，50+（x﹣50）×0.95=0.95x+2.5；
（2）当x为150时，小红在甲、乙两商场的实际花费相同；
（3）当小红累计购物超过100元而不到150元时，在乙商场实际花费少；正好为150元时，两商场花费相同；大于1... 直线l1：y=x+1与直线l2：y=mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为 ．
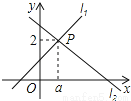
x≥1
【解析】
试题分析：首先把P（a，2）坐标代入直线y=x+1，求出a的值，从而得到P点坐标，再根据函数图象可得答案．
【解析】
将点P（a，2）坐标代入直线y=x+1，得a=1，
从图中直接看出，当x≥1时，x+1≥mx+n，
故答案为：x≥1． 若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（ ）
A. 7 B. 10 C. 35 D. 70
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式，即可得出关于n的一元一次方程，解方程即可求出n的值，将其代入中即可得出结论．
【解析】
∵一个正n边形的每个内角为144°，
∴144n=180×（n﹣2），解得：n=10．
这个正n边形的所有对角线的条数是：==35．
故选C．