��Ŀ����
��ͼ1���ı���ABCD�У�AD��BC����ABC=��DCB��AB=DC��
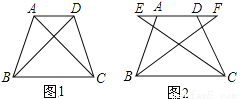
��1����֤��AC=DB��
��2����ͼ2��E��F����ͬʱ��A��D������ֱ��AD������ͬ���ٶȷ�����У�BF��CE���������֤����Ľ��ۡ�
 ��1��֤����������2��BF=CE
�����������������
��1���ɡ�ABC=��DCB��AB=DC���BC=CB����֤�ã���ABC�ա�DCB���Ӷ��ɵ�AC=DB��
��2��������ɵ�AE=DF���Ӷ��ɵ�AF=DE����AD��BC��ϡ�ABC=��DCB���á�BAD=��CDA���ٽ��AB=DC����֤�á�BAF�ա�CDE���Ӷ��ɵ�BF=CE.
���������
��1���ڡ�ABC�͡�DCB...
��1��֤����������2��BF=CE
�����������������
��1���ɡ�ABC=��DCB��AB=DC���BC=CB����֤�ã���ABC�ա�DCB���Ӷ��ɵ�AC=DB��
��2��������ɵ�AE=DF���Ӷ��ɵ�AF=DE����AD��BC��ϡ�ABC=��DCB���á�BAD=��CDA���ٽ��AB=DC����֤�á�BAF�ա�CDE���Ӷ��ɵ�BF=CE.
���������
��1���ڡ�ABC�͡�DCB...
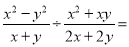 ___________
___________
 �����������������
�ʴ�Ϊ��
�����������������
�ʴ�Ϊ�� ����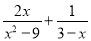 �Ľ���ǣ� ��
�Ľ���ǣ� ��
A. 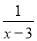 B.
B. 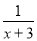 C.
C. 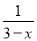 D.
D. 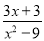
 B
��������ԭʽ=?===.
��ѡ��B.
B
��������ԭʽ=?===.
��ѡ��B. ͼ1����ʾ������м��㣺(1)�����룭3����y��ֵ��(2)����һ������x������Ľ����Ϊy1���ڶ�������(1��x)������Ľ����Ϊy2��Ҫʹy1��y2��������ѡ��x��ֵ������xֵ�ķ�Χ��ͼ2�е������ϱ�ʾ������

 ��1��-8����2��x��0.5.
���������������������1�����������Ϊx��������Ľ��y=2(x-1)����x=-3ʱ��y=-8��
��2��y1��2(x��1)��y2����2x���ָ���y1��y2���õ�2(x��1)����2x���ⲻ��ʽ��x��0.5���������������
�����������
(1)y��(x��1)��2��2(x��1)����x����3ʱ��y��2��(��3��1)����8��
(2)������֪y1��...
��1��-8����2��x��0.5.
���������������������1�����������Ϊx��������Ľ��y=2(x-1)����x=-3ʱ��y=-8��
��2��y1��2(x��1)��y2����2x���ָ���y1��y2���õ�2(x��1)����2x���ⲻ��ʽ��x��0.5���������������
�����������
(1)y��(x��1)��2��2(x��1)����x����3ʱ��y��2��(��3��1)����8��
(2)������֪y1��... ����ʽ3x��2��2x��3�Ľ⼯�������ϱ�ʾ��ȷ����( )
A.  B.
B. 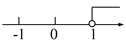 C.
C. 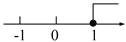 D.
D. 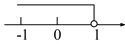
 D
����������������
3x+2��2x+3
����ϲ�ͬ�����
x��1����ѡD��
D
����������������
3x+2��2x+3
����ϲ�ͬ�����
x��1����ѡD�� ��ͼ����֪AC��BD�ཻ�ڵ�O��OA=OC��OB=OD����ͼ���ж��ٶ�������ȫ�ȣ�������
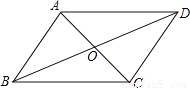
A. 1 B. 2 C. 3 D. 4
 D
����������AC��BD�ཻ�ڵ�O��
���AOD=��COB����AOB=��COD��
�֡�OA=OC��OB=OD��
���AOD�ա�COB����AOB�ա�COD��
��AD=CB��AB=CD��
�֡�AC=CA��BD=DB��
���ACD�ա�CAB����ABD�ա�CDB��
��ͼ�й���4��ȫ��������.
��ѡD.
D
����������AC��BD�ཻ�ڵ�O��
���AOD=��COB����AOB=��COD��
�֡�OA=OC��OB=OD��
���AOD�ա�COB����AOB�ա�COD��
��AD=CB��AB=CD��
�֡�AC=CA��BD=DB��
���ACD�ա�CAB����ABD�ա�CDB��
��ͼ�й���4��ȫ��������.
��ѡD. �����㡱�������������ڵĽ������ڽ��ŵؽ��У����д�����ɳʯ��Ҫ���䣮���氲��������������Ϊ8�֡�10�ֵĿ�����12����ȫ����������һ��������110��ɳʯ��
��1�����氲������������Ϊ8�֡�10�ֵĿ������ж�������
��2�����Ź��̵Ľ�չ�����氲��������Ҫһ������ɳʯ165�����ϣ�Ϊ����������������������ֿ�����6���������ж����ֹ���������һһд����
 ��������
��1���衰�氲������������Ϊ8�֡�10�ֵĿ����ֱ���x����y����
��������ã� ����ã� ��
�𣺡��氲������������Ϊ8�ֵĿ�����5����10�ֵĿ�����7����
��2����������Ϊ8�ֵĿ���������z����
������ã�8��5+z��+10��7+6��z����165����ã�z����
��z��0����������z=0��1��2��6��z=6��5��4��
��ӹ���3�ֹ���������
...
��������
��1���衰�氲������������Ϊ8�֡�10�ֵĿ����ֱ���x����y����
��������ã� ����ã� ��
�𣺡��氲������������Ϊ8�ֵĿ�����5����10�ֵĿ�����7����
��2����������Ϊ8�ֵĿ���������z����
������ã�8��5+z��+10��7+6��z����165����ã�z����
��z��0����������z=0��1��2��6��z=6��5��4��
��ӹ���3�ֹ���������
... �ⲻ��ʽ�����ѽ⼯�������ϱ�ʾ������
��1��5x��6��2��x+3����
��2��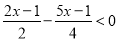
 ��1��x��4�� ��2��x����1��
���������������������1�����ݽ�һԪһ�β���ʽ�������裺ȥ���š�����ϲ�ͬ���ϵ����Ϊ1�ɵã�
��2�����ݽ�һԪһ�β���ʽ�������裺ȥ��ĸ��ȥ���š�����ϲ�ͬ���ϵ����Ϊ1�ɵã�
�������������1��ȥ���ţ��ã�5x��6��2x+6��
����ã�5x��2x��6+6��
�ϲ�ͬ����ã�3x��12��
ϵ����Ϊ1���ã�x��4��
...
��1��x��4�� ��2��x����1��
���������������������1�����ݽ�һԪһ�β���ʽ�������裺ȥ���š�����ϲ�ͬ���ϵ����Ϊ1�ɵã�
��2�����ݽ�һԪһ�β���ʽ�������裺ȥ��ĸ��ȥ���š�����ϲ�ͬ���ϵ����Ϊ1�ɵã�
�������������1��ȥ���ţ��ã�5x��6��2x+6��
����ã�5x��2x��6+6��
�ϲ�ͬ����ã�3x��12��
ϵ����Ϊ1���ã�x��4��
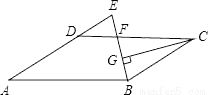
... ��ͼ����?ABCD�У�AB=12��AD=8����ABC��ƽ���߽�CD�ڵ�F����AD���ӳ����ڵ�E��CG��BE������ΪG����EF=2�����߶�CG�ij�Ϊ��������
A. 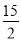 B.
B. 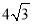 C.
C. 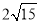 D.
D. 
 C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
��BG=BF=2...
C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
��BG=BF=2... 
