题目内容
如图，点B、D、E、C在一条直线上，△ABD≌△ACE，AB和AC，AD和AE是对应边，除△ABD≌△ACE外，图中还有其他全等三角形吗？若有，请写出来，并证明你的结论。
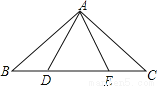
有，△ABE≌△ACD
【解析】试题分析：
由△ABD≌△ACE可得：AB=AC，BD=CE，∠B=∠C，从而易得BE=CD，这样由“SAS”即可证得△ABE和△ACD.
试题解析：
有，△ABE≌△ACD；理由如下：
∵△ABD≌△ACE，
∴AB=AC，BD=CE，∠B=∠C，
∴BE=CD，
在△ABE和△ACD中，
，
∴△ABE...
练习册系列答案
名校课堂系列答案
相关题目
分式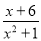
有意义的条件是____________
x可以取全体实数
【解析】试题解析：：因为恒大于0，所以x可以取全体实数.
故答案为：x可以取全体实数. 分式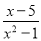
与
的公分母是（ ）
A. 
B. 
C. 
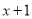D.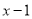 
A
【解析】试题分析：x2－1＝(x＋1)(x－1)，
所以分式与的公分母是(x＋1)(x－1)，
即x2－1．
故选A． 当正整数m为何值时，关于x的方程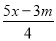
＝
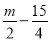的解是非正数？
m＝1或2或3.
【解析】【试题分析】求出不等式＝的解集为 ，再根据方程的解为非正数，得不等式m－3≤0，解不等式得：m≤3，因为m为正整数，m＝1或2或3.
【试题解析】
＝
去分母得：
移项得：
系数化为1 得：
又 m－3≤0，
∴m≤3，
∵m为正整数，
∴m＝1或2或3.
故答案为：m＝1或2或3. 在不等式
＞
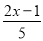的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x＞13.其中错误的步骤是( )
A. ① B. ②
C. ③ D. ④
D
【解析】＞的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x<13.故错误的步骤是④.故选D. 如图，下列条件能保证△ABC≌△ADC的是：①AB=AD，BC=DC；②∠1=∠3，∠4=∠2；③∠1=∠2，∠4=∠3；④∠1=∠2，AB=AD；⑤∠1=∠2，BC=DC．（ ）
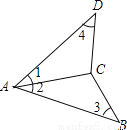
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
C
【解析】∵在△ABC和△ADC中，AC=AC，
∴当添加条件：①AB=AD，BC=DC时，可由“SSS”得到△ABC≌△ADC；
当添加条件：②∠1=∠3，∠4=∠2时，不能得到△ABC≌△ADC；
当添加条件：③∠1=∠2，∠4=∠3时，可由“AAS”得到△ABC≌△ADC；
当添加条件：④∠1=∠2，AB=AD时，可由“SAS”得到△ABC≌△ADC；
... 为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，现计划用210000元资金，购买这三种树共1000棵．
（1）求乙、丙两种树每棵各多少元？
（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？
（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？
（1）200元，200元，（2）能购买甲种树600棵，乙种树300棵，丙种树100棵；（3）丙种树最多可以购买201棵．
【解析】
试题分析：（1）利用已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，即可求出乙、丙两种树每棵钱数；
（2）假设购买乙种树x棵，则购买甲种树2x棵，丙种树（1000-3x）棵，利用（1）中所求树木价格以及现计划用210000元资金购买这三... 解不等式组：
（1）
；
（2）
．
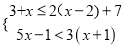（1）0＜x≤4；（2）0≤x＜2．
【解析】【试题分析】（1）分别求出每一个不等式的解集，根据口诀：大小小大中间找即可确定不等式组的解集；
（2）分别求出每一个不等式的解集，根据口诀：大小小大中间找即可确定不等式组的解集．
【试题解析】
（1）解不等式5x﹣6≤2（x+3），得：x≤4，
解不等式，得：x＞0，
∴不等式组的解集为0＜x≤4；
（2）解不... 如图，?ABCD的对角线AC，BD相交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为( )
A. 13 B. 17 C. 20 D. 26
B
【解析】试题分析：由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．
【解析】
∵四边形ABCD是平行四边形，
∴OA=OC=3，OB=OD=6，BC=AD=8，
∴△OBC的周长=OB+OC+AD=3+6+8=17．
故选：B．