��Ŀ����
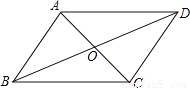
��ͼ����֪AC��BD�ཻ�ڵ�O��OA=OC��OB=OD����ͼ���ж��ٶ�������ȫ�ȣ�������
A. 1 B. 2 C. 3 D. 4
 D
����������AC��BD�ཻ�ڵ�O��
���AOD=��COB����AOB=��COD��
�֡�OA=OC��OB=OD��
���AOD�ա�COB����AOB�ա�COD��
��AD=CB��AB=CD��
�֡�AC=CA��BD=DB��
���ACD�ա�CAB����ABD�ա�CDB��
��ͼ�й���4��ȫ��������.
��ѡD.
D
����������AC��BD�ཻ�ڵ�O��
���AOD=��COB����AOB=��COD��
�֡�OA=OC��OB=OD��
���AOD�ա�COB����AOB�ա�COD��
��AD=CB��AB=CD��
�֡�AC=CA��BD=DB��
���ACD�ա�CAB����ABD�ա�CDB��
��ͼ�й���4��ȫ��������.
��ѡD.
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д����� 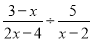 =_____________
=_____________
 �����������������
�ʴ�Ϊ��
�����������������
�ʴ�Ϊ�� ij��������ͼ����ʾ�ij����κ�������ֽ�壬������ͼ����ʾ����ʽ���ʽ���ֳ�������״����ֽ�У�

��1������������ֽ��162�ţ�������ֽ��340�ţ���Ҫ������ֽ�й�100����������ʽֽ��x����
�ٸ������⣬������±���
ֽ�� ֽ�� | ��ʽֽ�У����� | ��ʽֽ�У����� |
x | 100��x | |
������ֽ�壨�ţ� | 2��100��x�� | |
������ֽ�壨�ţ� | 4x |
�ڰ�����ֽ�е������������֣����ļ�������������
��2������������ֽ162�ţ�������ֽ��a�ţ�������������ֽ�У�ֽ��ǡ�����꣮��֪290��a��306����a��ֵ��
 ��1���ټ��������������ַ�����������ʽֽ��38������ʽֽ��62����������ʽֽ��39������ʽֽ��61����������ʽֽ��40������ʽֽ��60����
��2��293��298��303��д������һ�����ɣ���
�������������������1���ٿɸ�����ʽֽ��+��ʽֽ��=100����ÿ����ʽֽ����1��������ֽ���4��������ֽ�壬ÿ����ʽֽ����3��������ֽ���2��������ֽ������գ�
��������ʽֽ���õ�������ֽ��...
��1���ټ��������������ַ�����������ʽֽ��38������ʽֽ��62����������ʽֽ��39������ʽֽ��61����������ʽֽ��40������ʽֽ��60����
��2��293��298��303��д������һ�����ɣ���
�������������������1���ٿɸ�����ʽֽ��+��ʽֽ��=100����ÿ����ʽֽ����1��������ֽ���4��������ֽ�壬ÿ����ʽֽ����3��������ֽ���2��������ֽ������գ�
��������ʽֽ���õ�������ֽ��... ����ʽ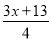 ��
��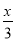 ��2�Ľ���_________.
��2�Ľ���_________.
 x����3
������������2, ȥ��ĸ�ã� ȥ���ŵã� ����ϲ��ã� ϵ����Ϊ1�ã� .
�ʴ�Ϊx����3.
x����3
������������2, ȥ��ĸ�ã� ȥ���ŵã� ����ϲ��ã� ϵ����Ϊ1�ã� .
�ʴ�Ϊx����3. ��ͼ1���ı���ABCD�У�AD��BC����ABC=��DCB��AB=DC��
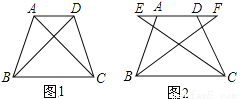
��1����֤��AC=DB��
��2����ͼ2��E��F����ͬʱ��A��D������ֱ��AD������ͬ���ٶȷ�����У�BF��CE���������֤����Ľ��ۡ�
 ��1��֤����������2��BF=CE
�����������������
��1���ɡ�ABC=��DCB��AB=DC���BC=CB����֤�ã���ABC�ա�DCB���Ӷ��ɵ�AC=DB��
��2��������ɵ�AE=DF���Ӷ��ɵ�AF=DE����AD��BC��ϡ�ABC=��DCB���á�BAD=��CDA���ٽ��AB=DC����֤�á�BAF�ա�CDE���Ӷ��ɵ�BF=CE.
���������
��1���ڡ�ABC�͡�DCB...
��1��֤����������2��BF=CE
�����������������
��1���ɡ�ABC=��DCB��AB=DC���BC=CB����֤�ã���ABC�ա�DCB���Ӷ��ɵ�AC=DB��
��2��������ɵ�AE=DF���Ӷ��ɵ�AF=DE����AD��BC��ϡ�ABC=��DCB���á�BAD=��CDA���ٽ��AB=DC����֤�á�BAF�ա�CDE���Ӷ��ɵ�BF=CE.
���������
��1���ڡ�ABC�͡�DCB... С�ܵ�ѧУʳ��������A��B������ǰ���Ŷӵ���һ����(��Ϊa�ˣ�a��8������վ��A���ڶ���ĺ��棬����2���ӣ�������A����ÿ������4�����˷��뿪���飬B����ÿ������6�����˷��뿪���飬��B���ڶ������ÿ��������5�ˣ�
��1����ʱ����С�ܼ�����A�����Ŷӣ��������ﴰ��������ʱ���Ƕ��٣����ú�a�Ĵ���ʽ��ʾ��
��2����ʱ����С��Ѹ�ٴ�A���ڶ���ת�Ƶ�B���ں��������Ŷӣ��ҵ���B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���٣���a��ȡֵ��Χ�����������������أ�
 ��1���֣���2��a��20
��������
�����������1�����ݡ�����2���ӣ�������A����ÿ������4�����˷��뿪���顱�����г�����ʽ��
��2�����ݡ�����B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���١������в���ʽ���.
��1�����������������A�����Ŷӵ��ﴰ��������ʱ��Ϊ�֣�
��2�����������a��20.
��1���֣���2��a��20
��������
�����������1�����ݡ�����2���ӣ�������A����ÿ������4�����˷��뿪���顱�����г�����ʽ��
��2�����ݡ�����B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���١������в���ʽ���.
��1�����������������A�����Ŷӵ��ﴰ��������ʱ��Ϊ�֣�
��2��������ã����a��20. ij���˴������г�����20ǧ���⣬ÿǧ��aԪ���ִ��������10ǧ���⣬ÿǧ��bԪ�����������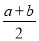 Ԫ�ĵ��۰���ȫ���������������Ǯ��ԭ���ǣ�������
Ԫ�ĵ��۰���ȫ���������������Ǯ��ԭ���ǣ�������
A. a��b B. a��b C. a=b D. ��a��b�Ĵ�С��
 A
����������������
����������20a+10b����30��= = =��
��a��b����a��b��0ʱ�������Ǯ����ѡA��
A
����������������
����������20a+10b����30��= = =��
��a��b����a��b��0ʱ�������Ǯ����ѡA�� ����ʽ�驁1��x��5��11�Ľ⼯��_________��
 4��x��16
������������ʽÿ�����ֶ���5�ã�4��x��16��
�ʴ�Ϊ��4��x��16��
4��x��16
������������ʽÿ�����ֶ���5�ã�4��x��16��
�ʴ�Ϊ��4��x��16�� ��ͼ���ڡ�ABC�У�AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ����ı���BEDF���ܳ��ǣ� ��

A��5 B��7 C��8 D��10
 D��
��������
�����������AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ���DE=AB=2��DF=BC=3��DE��BF��DF��BE�����ı���BEDFΪƽ���ı��Σ����ı���BEDF���ܳ�Ϊ��2��2+3��2=10����ѡD��
D��
��������
�����������AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ���DE=AB=2��DF=BC=3��DE��BF��DF��BE�����ı���BEDFΪƽ���ı��Σ����ı���BEDF���ܳ�Ϊ��2��2+3��2=10����ѡD�� 
