��Ŀ����
��ͼ����֪AB��CD��AE=CF�������������в�һ����ʹ��ABE�ա�CDF���ǣ�������

A. AB=CD B. BE��DF C. ��B=��D D. BE=DF
 D
����������AB��CD��
���A=��C��
�֡�AE=CF��
�ࣨ1�����ӡ�AB=CD�������ɡ�SAS���ж���ABE�ա�CDF��
��2�����ӡ�BE��DF���ɵá�FEB=��EFD����һ���ɵá�AEB=��CFD���Ӷ����ɡ�ASA���ж���ABE�ա�CDF��
��3�����ӡ���B=��D�����ɡ�AAS���ж���ABE�ա�CDF��
��4�����ӡ�BE=DF�������ж���ABE��...
D
����������AB��CD��
���A=��C��
�֡�AE=CF��
�ࣨ1�����ӡ�AB=CD�������ɡ�SAS���ж���ABE�ա�CDF��
��2�����ӡ�BE��DF���ɵá�FEB=��EFD����һ���ɵá�AEB=��CFD���Ӷ����ɡ�ASA���ж���ABE�ա�CDF��
��3�����ӡ���B=��D�����ɡ�AAS���ж���ABE�ա�CDF��
��4�����ӡ�BE=DF�������ж���ABE��...
��ʽ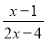 ��ֵΪ���������____________
��ֵΪ���������____________
 ���������������������Ϊ��ʽ��ֵΪ0��ʱ��ֻ���Ƿ���Ϊ0����ĸ����Ϊ0�����Կ��Եõ��� �����Եõ���
�ʴ�Ϊ�� .
���������������������Ϊ��ʽ��ֵΪ0��ʱ��ֻ���Ƿ���Ϊ0����ĸ����Ϊ0�����Կ��Եõ��� �����Եõ���
�ʴ�Ϊ�� . ij���ϳ���300ǧ�˵�A�ֹ�֭��240ǧ�˵�B�ֹ�֭Ϊԭ�ϣ����������ס��������������ϣ���֪ÿǧ�˼������Ϻ�0.6ǧ��A�ֹ�֭����0.3ǧ��B�ֹ�֭��ÿǧ���������Ϻ�0.2ǧ��A�ֹ�֭����0.4ǧ��B�ֹ�֭�����ϳ��ƻ������ס��������������Ϲ�650ǧ�ˣ���ó�������������x��ǧ�ˣ���
��1���г���������Ĺ���x�IJ���ʽ�飬�����x��ȡֵ��Χ��
��2����֪�����ϳ��ļ����������ۼ���ÿ1ǧ��3Ԫ�������������ۼ���ÿ1ǧ��4Ԫ����ô�����ϳ������ס����������ϸ�����ǧ�ˣ�����ʹ���������������ܽ�����
 ��������
��1����ó�������������xǧ�ˣ��������������ϣ�650��x��ǧ�ˣ�
����������
�ɢٵã�x��425���ɢڵã�x��200��
��x��ȡֵ��Χ��200��x��425��
��2�����������������ܽ��ΪyԪ����������ã�
����y=��x+2600��
��k=��1��0��
�൱x=200ʱ���������������ܽ�����Ϊ��200+2600=2400Ԫ��
������...
��������
��1����ó�������������xǧ�ˣ��������������ϣ�650��x��ǧ�ˣ�
����������
�ɢٵã�x��425���ɢڵã�x��200��
��x��ȡֵ��Χ��200��x��425��
��2�����������������ܽ��ΪyԪ����������ã�
����y=��x+2600��
��k=��1��0��
�൱x=200ʱ���������������ܽ�����Ϊ��200+2600=2400Ԫ��
������... �ڲ���ʽ ��
��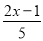 �ı��ι����У���ȥ��ĸ����5(2��x)��3(2x��1)����ȥ���ţ���10��5x��6x��3���������5x��6x����3��10����ϵ����Ϊ1����x��13.���д���IJ�����( )
�ı��ι����У���ȥ��ĸ����5(2��x)��3(2x��1)����ȥ���ţ���10��5x��6x��3���������5x��6x����3��10����ϵ����Ϊ1����x��13.���д���IJ�����( )
A. �� B. ��
C. �� D. ��
 D
�����������ı��ι����У���ȥ��ĸ����5(2��x)��3(2x��1)����ȥ���ţ���10��5x��6x��3���������5x��6x����3��10����ϵ����Ϊ1����x<13.�ʴ���IJ����Ǣ�.��ѡD.
D
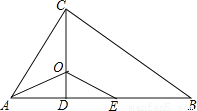
�����������ı��ι����У���ȥ��ĸ����5(2��x)��3(2x��1)����ȥ���ţ���10��5x��6x��3���������5x��6x����3��10����ϵ����Ϊ1����x<13.�ʴ���IJ����Ǣ�.��ѡD. ��ͼ����ABC�У���ACB=90�㣬CD��AB�ڵ�D��AOƽ�֡�BAC����CD�ڵ�O��EΪAB��һ�㣬��AE=AC��
��1����֤����AOC�ա�A0E��
��2����֤��OE��BC��
 ��1��֤����������2��֤��������
�����������������
��1����AOƽ�֡�BAC���ɵá�CAO=��EAO���AO=AO��AE=AC�����ɡ�SAS��֤�ã���AOC�ա�AOE��
��2���ɡ�AOC�ա�AOE�ɵá�ACO=��AEO���ɡ�ACB=90�㣬CD��AB�ڵ�D���á�ACO+��DCB=90�㣬��AEO+��EOD=90�㣬�Ӷ��ɵá�DCB=��DOE�����ɵõ���OE��BC.
����...
��1��֤����������2��֤��������
�����������������
��1����AOƽ�֡�BAC���ɵá�CAO=��EAO���AO=AO��AE=AC�����ɡ�SAS��֤�ã���AOC�ա�AOE��
��2���ɡ�AOC�ա�AOE�ɵá�ACO=��AEO���ɡ�ACB=90�㣬CD��AB�ڵ�D���á�ACO+��DCB=90�㣬��AEO+��EOD=90�㣬�Ӷ��ɵá�DCB=��DOE�����ɵõ���OE��BC.
����... Ϊ��һ�������������˾ӵ���̬������ij��������ס��ҡ���������������ׯ����֪�ס��ұ��������ļ۸�֮��Ϊ2��2��3��������ÿ��200Ԫ���ּƻ���210000Ԫ�ʽ𣬹�������������1000�ã�
��1�����ҡ���������ÿ�ø�����Ԫ��
��2��������������Ŀ�������������2����ǡ������ƻ��ʽ��������������ܹ�����ٿã�
��3������������10120Ԫ�Ĺ�����ڹ����ܿ��������ǰ���£�������������Թ�����ٿã�
 ��1��200Ԫ��200Ԫ����2���ܹ��������600�ã�������300�ã�������100�ã���3�������������Թ���201�ã�
��������
�����������1��������֪�ס��ұ��������ļ۸�֮��Ϊ2��2��3��������ÿ��200Ԫ����������ҡ���������ÿ��Ǯ����
��2�����蹺��������x�ã����������2x�ã���������1000-3x���ã����ã�1����������ľ�۸��Լ��ּƻ���210000Ԫ�ʽ�������...
��1��200Ԫ��200Ԫ����2���ܹ��������600�ã�������300�ã�������100�ã���3�������������Թ���201�ã�
��������
�����������1��������֪�ס��ұ��������ļ۸�֮��Ϊ2��2��3��������ÿ��200Ԫ����������ҡ���������ÿ��Ǯ����
��2�����蹺��������x�ã����������2x�ã���������1000-3x���ã����ã�1����������ľ�۸��Լ��ּƻ���210000Ԫ�ʽ�������... ij�糡Ϊϣ���������ݵ����ձ�����60Ԫ��100Ԫ����Ʊ�ۣ�ij�����蹺��140�ţ�����Ʊ��Ϊ100Ԫ��Ʊ��������Ʊ��Ϊ60Ԫ��Ʊ��������������������Ʊ���ٹ���Ҫ��������
A. 12120Ԫ B. 12140Ԫ C. 12160Ԫ D. 12200Ԫ
 C
����������������
��Ʊ��Ϊ60Ԫ��Ʊ��Ϊx�ţ�Ʊ��Ϊ100Ԫ��Ʊ��Ϊy�ţ���������ã� ���ɵã�x�ܣ�
�������֪��x��yΪ����������x=46��y=94��
���������Ʊ������Ҫ60��46+100��94=12160��
��ѡC��
C
����������������
��Ʊ��Ϊ60Ԫ��Ʊ��Ϊx�ţ�Ʊ��Ϊ100Ԫ��Ʊ��Ϊy�ţ���������ã� ���ɵã�x�ܣ�
�������֪��x��yΪ����������x=46��y=94��
���������Ʊ������Ҫ60��46+100��94=12160��
��ѡC�� С��88����λ�����������ĸ�λ���ֱ�ʮλ���ִ�4����������λ����_________����
 5
����������ʮλ����Ϊx�����λ����Ϊx+4
�������10x+x+4��88
��x��
�֡�xӦΪ���������Ҵ���0������0�ܸ�λ���֡�9�����5��x+4��9
��1��x��5���������������5����
�ʴ𰸣�5.
5
����������ʮλ����Ϊx�����λ����Ϊx+4
�������10x+x+4��88
��x��
�֡�xӦΪ���������Ҵ���0������0�ܸ�λ���֡�9�����5��x+4��9
��1��x��5���������������5����
�ʴ𰸣�5. �����������У��ܹ��ж�һ���ı�����ƽ���ı��ε��ǣ�������
A. һ��Ա�ƽ�У���һ��Ա����
B. һ��Ա���ȣ�һ��Խ����
C. һ��Ա�ƽ�У�һ���Խ���ƽ����һ���Խ���
D. һ��Ա���ȣ�һ���Խ���ƽ����һ���Խ���
 C
��������A����������ı����п����ǵ������Σ�
B����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
C����ȷ����������������ȫ��֤��ƽ�е�һ��Ա���ȣ�����ƽ���ı��Σ�
D����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
��ѡC��
C
��������A����������ı����п����ǵ������Σ�
B����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
C����ȷ����������������ȫ��֤��ƽ�е�һ��Ա���ȣ�����ƽ���ı��Σ�
D����������������ȫ�ȵ���������֤����ȵ�һ��Ա�ƽ�У�
��ѡC�� 
