下列不等式中,是一元一次不等式的是( )
A. 2x-1>0 B. -1<2 C. 3x-2y≤-1 D. y2+3>5
 A
【解析】A、是一元一次不等式;
B、不含未知数,不符合定义;
C、含有两个未知数,不符合定义;
D、未知数的次数是2,不符合定义;
故选A.
A
【解析】A、是一元一次不等式;
B、不含未知数,不符合定义;
C、含有两个未知数,不符合定义;
D、未知数的次数是2,不符合定义;
故选A. 若 x2m-1-8>5是一元一次不等式,则m的值为( )
x2m-1-8>5是一元一次不等式,则m的值为( )
A. 0 B. 1
C. 2 D. 3
 B
【解析】根据一元一次不等式的定义得: ,故选B.
B
【解析】根据一元一次不等式的定义得: ,故选B. 不等式3x+2<2x+3的解集在数轴上表示正确的是( )
A.  B.
B. 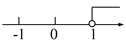 C.
C. 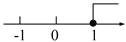 D.
D. 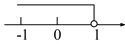
 D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D.
D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D. 在不等式 >
>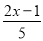 的变形过程中:①去分母,得5(2+x)>3(2x-1);②去括号,得10+5x>6x-3;③移项得5x-6x>-3-10;④系数化为1,得x>13.其中错误的步骤是( )
的变形过程中:①去分母,得5(2+x)>3(2x-1);②去括号,得10+5x>6x-3;③移项得5x-6x>-3-10;④系数化为1,得x>13.其中错误的步骤是( )
A. ① B. ②
C. ③ D. ④
 D
【解析】>的变形过程中:①去分母,得5(2+x)>3(2x-1);②去括号,得10+5x>6x-3;③移项得5x-6x>-3-10;④系数化为1,得x<13.故错误的步骤是④.故选D.
D
【解析】>的变形过程中:①去分母,得5(2+x)>3(2x-1);②去括号,得10+5x>6x-3;③移项得5x-6x>-3-10;④系数化为1,得x<13.故错误的步骤是④.故选D. 不等式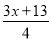 >
>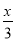 +2的解是_________.
+2的解是_________.
 x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3.
x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3. 如果不等式ax+4<0的解集在数轴上表示如图,那么a的值为____.

 -2
【解析】解不等式ax+4<0得, 由数轴上可得:不等式的解集为: ,则 解得: .
故答案为
-2
【解析】解不等式ax+4<0得, 由数轴上可得:不等式的解集为: ,则 解得: .
故答案为 按要求解答下列各题:
(1)解不等式:3x-5<2(2+3x);
(2)解不等式:2x-3≤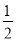 (x+2);
(x+2);
(3)解不等式:  <x-1,并将解集在数轴上表示出来.
<x-1,并将解集在数轴上表示出来.
 (1)x>-3 (2)x≤ (3)x>2,画数轴略
【解析】【试题分析】(1)去括号得: 移项得: 合并同类项得: 系数化为1得:x>-3 ;
(2) 去括号得: 移项得: 合并同类项得: 系数化为1得: x≤ ;
(3)去分母得: 移项得: ,合并得: 系数化为1得:x>2,数轴见解析.
【试题解析】
去括号得:
移项得:
合并同类项得:
系数化为...
(1)x>-3 (2)x≤ (3)x>2,画数轴略
【解析】【试题分析】(1)去括号得: 移项得: 合并同类项得: 系数化为1得:x>-3 ;
(2) 去括号得: 移项得: 合并同类项得: 系数化为1得: x≤ ;
(3)去分母得: 移项得: ,合并得: 系数化为1得:x>2,数轴见解析.
【试题解析】
去括号得:
移项得:
合并同类项得:
系数化为... 求出不等式3x-2≥4(x-1)的所有非负整数解.
 不等式的解集是x≤2,故不等式3x-2≥4(x-1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得: 移项得: 合并得: ,系数化为1得:x≤2,所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得:
移项得:
合并得: ,
系数化为1得:x≤2,
所以不等式的非负整数解为0,1,2.
不等式的解集是x≤2,故不等式3x-2≥4(x-1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得: 移项得: 合并得: ,系数化为1得:x≤2,所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得:
移项得:
合并得: ,
系数化为1得:x≤2,
所以不等式的非负整数解为0,1,2. x取什么值时,代数式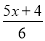 的值不小于
的值不小于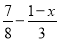 的值?并求x的最小值.
的值?并求x的最小值.
 x≥-,最小值为-.
【解析】【试题分析】根据题意,列出不等式 ,求出不等式的解集x≥-即可.
【试题解析】
由题意得:
,
去分母得: ,
去括号得:
移项得:
合并同类项得: 系数化为1得: .
x的最小值为-.
故答案为x≥-,最小值为-.
x≥-,最小值为-.
【解析】【试题分析】根据题意,列出不等式 ,求出不等式的解集x≥-即可.
【试题解析】
由题意得:
,
去分母得: ,
去括号得:
移项得:
合并同类项得: 系数化为1得: .
x的最小值为-.
故答案为x≥-,最小值为-. 图1中所示程序进行计算:(1)若输入-3,求y的值;(2)若第一次输入x,输出的结果记为y1,第二次输入(1-x),计算的结果记为y2,要使y1>y2,你怎样选择x的值,并把x值的范围在图2中的数轴上表示出来.

 (1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=...
(1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=...