题目内容
在不等式
＞
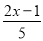的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x＞13.其中错误的步骤是( )
A. ① B. ②
C. ③ D. ④
D
【解析】＞的变形过程中：①去分母，得5(2＋x)＞3(2x－1)；②去括号，得10＋5x＞6x－3；③移项得5x－6x＞－3－10；④系数化为1，得x<13.故错误的步骤是④.故选D.
练习册系列答案
相关题目
化简分式：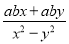 
.
．
【解析】试题分析：先把分子分母分解因式，然后再约分．
试题解析：【解析】
原式==． 把分式
中的m和n都扩大4倍，那么分式的值（ ）
A. 也扩大4倍 B. 扩大为原来的4倍 C. 不变 D. 缩小为原来的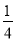
C
【解析】试题分析：把分式中的m、n分别用4m、4n代替，
得＝＝，
所以分式的值不变，
故选C． 一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2，则x的取值范围是__．
10＜x＜30
【解析】【解析】
矩形的周长是2（x+10）cm，面积是10xcm2．根据题意，得：
，
解不等式：2（x+10）＜80，
解得：x＜30，
解不等式：10x＞100，
解得：x＞10，
所以x的取值范围是：10＜x＜30．
故答案为：10＜x＜30． x取什么值时，代数式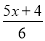
的值不小于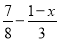
的值？并求x的最小值．
x≥－，最小值为－.
【解析】【试题分析】根据题意，列出不等式 ，求出不等式的解集x≥－即可.
【试题解析】
由题意得：
，
去分母得： ，
去括号得：
移项得：
合并同类项得： 系数化为1得： .
x的最小值为－.
故答案为x≥－，最小值为－. 如图，点B、D、E、C在一条直线上，△ABD≌△ACE，AB和AC，AD和AE是对应边，除△ABD≌△ACE外，图中还有其他全等三角形吗？若有，请写出来，并证明你的结论。
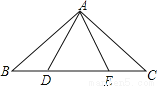
有，△ABE≌△ACD
【解析】试题分析：
由△ABD≌△ACE可得：AB=AC，BD=CE，∠B=∠C，从而易得BE=CD，这样由“SAS”即可证得△ABE和△ACD.
试题解析：
有，△ABE≌△ACD；理由如下：
∵△ABD≌△ACE，
∴AB=AC，BD=CE，∠B=∠C，
∴BE=CD，
在△ABE和△ACD中，
，
∴△ABE... 如图，已知AB∥CD，AE=CF，则下列条件中不一定能使△ABE≌△CDF的是（ ）
A. AB=CD B. BE∥DF C. ∠B=∠D D. BE=DF
D
【解析】∵AB∥CD，
∴∠A=∠C，
又∵AE=CF，
∴（1）添加“AB=CD”，可由“SAS”判定△ABE≌△CDF；
（2）添加“BE∥DF”可得∠FEB=∠EFD，进一步可得∠AEB=∠CFD，从而可由“ASA”判定△ABE≌△CDF；
（3）添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF；
（4）添加“BE=DF”不能判定△ABE≌... 甲、乙原有存款800元和1800元，从本月开始，甲每月存400元，乙每月存200元．如果设两人存款时间为x月．甲存款额是y1元，乙存款额是y2元．
（1）试写出y1与x及y2与x之间的函数关系式；
（2）到第几个月时，甲存款额能超过乙存款额？
详见解析
【解析】
试题分析：（1）根据存款数=原有存款+又存入的钱数，列式即可；
（2）列出一元一次不等式，然后求解即可．
【解析】
（1）根据题意，甲：y1=400x+800，
乙：y2=200x+1800；
（2）根据题意，400x+800＞200x+1800，
解得x＞5，
所以，从第6个月开始，甲存款额能超过乙存款额． 一个多边形的内角和是外角和的2倍，则这个多边形的边数为______．
6
【解析】∵多边形的外角和是360度，多边形的内角和是外角和的2倍，
则内角和是720度，
720÷180+2=6，
∴这个多边形是六边形，
故答案为：6．