题目内容
不等式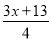 >
>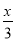 +2的解是_________.
+2的解是_________.
 x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3.
x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3.
练习册系列答案
相关题目
“a是有理数,|a|≥0”这一事件是( )
A. 必然事件 B. 随机事件
C. 不可能事件 D. 都不是
 A
【解析】∵a是有理数,
∴|a|≥0是必然事件.
故选A.
A
【解析】∵a是有理数,
∴|a|≥0是必然事件.
故选A. 下列各式与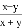 相等的是( )
相等的是( )
A. 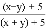 B.
B. 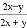
C. 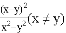 D.
D. 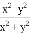
 C
【解析】试题分析:因为不能约分,所以,所以A错误;因为不能约分,所以,所以B错误;因为,所以C正确;因为不能约分,所以,所以D错误;故选:C.
C
【解析】试题分析:因为不能约分,所以,所以A错误;因为不能约分,所以,所以B错误;因为,所以C正确;因为不能约分,所以,所以D错误;故选:C. 有一个两位数,其个位数字比十位数字大2,已知这个两位数大于20且小于40,那么这个两位数是__.
 24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35.
24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35. 图1中所示程序进行计算:(1)若输入-3,求y的值;(2)若第一次输入x,输出的结果记为y1,第二次输入(1-x),计算的结果记为y2,要使y1>y2,你怎样选择x的值,并把x值的范围在图2中的数轴上表示出来.

 (1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=...
(1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=... 如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
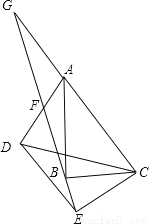
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
 (1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A...
(1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A... 如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等( )
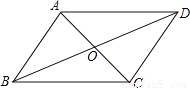
A. 1 B. 2 C. 3 D. 4
 D
【解析】∵AC与BD相交于点O,
∴∠AOD=∠COB,∠AOB=∠COD,
又∵OA=OC,OB=OD,
∴△AOD≌△COB,△AOB≌△COD,
∴AD=CB,AB=CD,
又∵AC=CA,BD=DB,
∴△ACD≌△CAB,△ABD≌△CDB,
即图中共有4对全等三角形.
故选D.
D
【解析】∵AC与BD相交于点O,
∴∠AOD=∠COB,∠AOB=∠COD,
又∵OA=OC,OB=OD,
∴△AOD≌△COB,△AOB≌△COD,
∴AD=CB,AB=CD,
又∵AC=CA,BD=DB,
∴△ACD≌△CAB,△ABD≌△CDB,
即图中共有4对全等三角形.
故选D. 在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
 (1)每台电脑0.5万元,每台电子白板1.5万元;(2)方案3最省钱,即购买电脑17台,电子白板13台最省
【解析】试题分析:(1)先设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元列出方程组,求出x,y的值即可;
(2)先设需购进电脑a台,则购进电子白板(30﹣a)台,根据需购进电脑和电子白板共30台,总费用...
(1)每台电脑0.5万元,每台电子白板1.5万元;(2)方案3最省钱,即购买电脑17台,电子白板13台最省
【解析】试题分析:(1)先设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元列出方程组,求出x,y的值即可;
(2)先设需购进电脑a台,则购进电子白板(30﹣a)台,根据需购进电脑和电子白板共30台,总费用... 如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是_______.
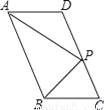
 24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD...
24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD... 
