题目内容
不等式3x+2<2x+3的解集在数轴上表示正确的是( )
A.  B.
B. 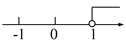 C.
C. 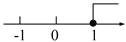 D.
D. 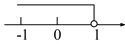
 D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D.
D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
计算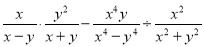
 【解析】试题分析:分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析:
原式=
【解析】试题分析:分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析:
原式= 计算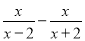 的结果是( )
的结果是( )
A. -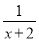 B.
B. 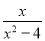 C.
C. 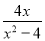 D.
D. 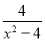
 C
【解析】试题分析:原式=
=
=.
故选C.
C
【解析】试题分析:原式=
=
=.
故选C. 现有球迷150人欲同时租用A,B,C三种型号客车去观看世界杯足球赛,其中A,B,C三种型号客车载容量分别为50人,30人,10人,要求每辆车必须满载,其中A型客车最多租两辆,则球迷们一次性到达赛场的租车方案有( )
A. 3种 B. 4种 C. 5种 D. 6种
 B
【解析】此题首先注意租用A型号客车时分两种情况讨论,进而列出方程,再进一步根据车辆数是整数进行分析.
【解析】
设B、C两种车分别租a辆、b辆.
①当A型号租用1辆时,则有
30a+10b=150﹣50,
3a+b=10.
又a,b是整数,
则a=1,b=7或a=2,b=4或a=3,b=1.
②当A型号租用2辆时,则有
30a+10b=1...
B
【解析】此题首先注意租用A型号客车时分两种情况讨论,进而列出方程,再进一步根据车辆数是整数进行分析.
【解析】
设B、C两种车分别租a辆、b辆.
①当A型号租用1辆时,则有
30a+10b=150﹣50,
3a+b=10.
又a,b是整数,
则a=1,b=7或a=2,b=4或a=3,b=1.
②当A型号租用2辆时,则有
30a+10b=1... 求出不等式3x-2≥4(x-1)的所有非负整数解.
 不等式的解集是x≤2,故不等式3x-2≥4(x-1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得: 移项得: 合并得: ,系数化为1得:x≤2,所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得:
移项得:
合并得: ,
系数化为1得:x≤2,
所以不等式的非负整数解为0,1,2.
不等式的解集是x≤2,故不等式3x-2≥4(x-1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得: 移项得: 合并得: ,系数化为1得:x≤2,所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得:
移项得:
合并得: ,
系数化为1得:x≤2,
所以不等式的非负整数解为0,1,2. 如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
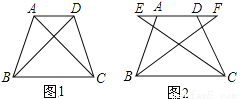
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
 (1)证明见解析(2)BF=CE
【解析】试题分析:
(1)由∠ABC=∠DCB,AB=DC结合BC=CB即可证得:△ABC≌△DCB,从而可得AC=DB;
(2)由题意可得AE=DF,从而可得AF=DE,由AD∥BC结合∠ABC=∠DCB,易得∠BAD=∠CDA,再结合AB=DC即可证得△BAF≌△CDE,从而可得BF=CE.
试题解析:
(1)在△ABC和△DCB...
(1)证明见解析(2)BF=CE
【解析】试题分析:
(1)由∠ABC=∠DCB,AB=DC结合BC=CB即可证得:△ABC≌△DCB,从而可得AC=DB;
(2)由题意可得AE=DF,从而可得AF=DE,由AD∥BC结合∠ABC=∠DCB,易得∠BAD=∠CDA,再结合AB=DC即可证得△BAF≌△CDE,从而可得BF=CE.
试题解析:
(1)在△ABC和△DCB... 如图,已知AB=AD给出下列条件:
(1)CB=CD (2)∠BAC=∠DAC (3)∠BCA=∠DCA (4)∠B=∠D,
若再添一个条件后,能使△ABC≌△ADC的共有( )
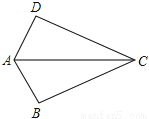
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】∵在△ABC和△ADC中,AB=AD,AC=AC,
∴(1)添加“CB=CD”可由“SSS”判定△ABC≌△ADC;
(2)添加“∠BAC=∠DAC”可由“SAS”判定△ABC≌△ADC;
(3)添加“∠BCA=∠DCA”不能判定△ABC≌△ADC;
(4)添加“∠B=∠D”不能判定△ABC≌△ADC;
即4个条件中,添加(1)和(2)能使△ABC≌...
B
【解析】∵在△ABC和△ADC中,AB=AD,AC=AC,
∴(1)添加“CB=CD”可由“SSS”判定△ABC≌△ADC;
(2)添加“∠BAC=∠DAC”可由“SAS”判定△ABC≌△ADC;
(3)添加“∠BCA=∠DCA”不能判定△ABC≌△ADC;
(4)添加“∠B=∠D”不能判定△ABC≌△ADC;
即4个条件中,添加(1)和(2)能使△ABC≌... 每年3月12日是植树节,某学校植树小组若干人植树,植树若干棵.若每人植4棵,则余20棵没人植,若每人植8棵,则有一人比其他人植的少(但有树植),问这个植树小组有多少人?共有多少棵树?
 这个植树小组有6人去植树,共有4×6+20=44棵树.
【解析】【试题分析】设该校一共有x人去植树,共有y棵树.则根据题意可得:,求解即得
【试题解析】设个植树小组有x人去植树,共有y棵树.
由“每人植4棵,则余20棵没人植”和“若每人植8棵,则有一人比其他人植的少(但有树植)”得:
,将y=4x+20代入第二个式子得:
0<4x+20﹣8(x﹣1)<8,
5<...
这个植树小组有6人去植树,共有4×6+20=44棵树.
【解析】【试题分析】设该校一共有x人去植树,共有y棵树.则根据题意可得:,求解即得
【试题解析】设个植树小组有x人去植树,共有y棵树.
由“每人植4棵,则余20棵没人植”和“若每人植8棵,则有一人比其他人植的少(但有树植)”得:
,将y=4x+20代入第二个式子得:
0<4x+20﹣8(x﹣1)<8,
5<... 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
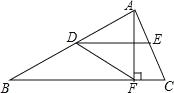
A.4 B.8 C.2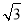 D.4
D.4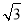
 D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D.
D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D. 
