题目内容
求出不等式3x-2≥4(x-1)的所有非负整数解.
 不等式的解集是x≤2,故不等式3x-2≥4(x-1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得: 移项得: 合并得: ,系数化为1得:x≤2,所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得:
移项得:
合并得: ,
系数化为1得:x≤2,
所以不等式的非负整数解为0,1,2.
不等式的解集是x≤2,故不等式3x-2≥4(x-1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得: 移项得: 合并得: ,系数化为1得:x≤2,所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得:
移项得:
合并得: ,
系数化为1得:x≤2,
所以不等式的非负整数解为0,1,2.
下列事件中的不可能事件是( )
A. 通常加热到100 ℃时,水沸腾
B. 抛掷2枚正方体骰子,都是6点朝上
C. 经过有交通信号灯的路口,遇到红灯
D. 任意画一个三角形,其内角和是360°
 D
【解析】A. 是必然事件,选项错误;
B. 是随机事件,选项错误;
C. 是随机事件,选项错误;
D. 是不可能事件,选项正确。
故选:D.
D
【解析】A. 是必然事件,选项错误;
B. 是随机事件,选项错误;
C. 是随机事件,选项错误;
D. 是不可能事件,选项正确。
故选:D. 计算 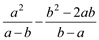 的值是___________
的值是___________
 【解析】试题分析:
=
=
=a-b.
故答案为:a-b.
【解析】试题分析:
=
=
=a-b.
故答案为:a-b. 如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的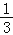 ,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a(cm),若铁钉总长度为6(cm),则a的取值范围是__.
,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a(cm),若铁钉总长度为6(cm),则a的取值范围是__.

 ≤a<
【解析】【解析】
∵每次钉入木块的钉子长度是前一次的.已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后铁钉进入木块的长度是a(cm),
根据题意得:敲击2次后铁钉进入木块的长度是a+a=a(cm),
而此时还要敲击1次,∵铁钉总长度为6cm,故a<6,
第三次敲击进去最大长度是前一次的,也就是第二次的=a(cm),
∴ ,
∴a的取值...
≤a<
【解析】【解析】
∵每次钉入木块的钉子长度是前一次的.已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后铁钉进入木块的长度是a(cm),
根据题意得:敲击2次后铁钉进入木块的长度是a+a=a(cm),
而此时还要敲击1次,∵铁钉总长度为6cm,故a<6,
第三次敲击进去最大长度是前一次的,也就是第二次的=a(cm),
∴ ,
∴a的取值... 甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是( )
A. 1℃~3℃ B. 3℃~5℃ C. 5℃~8℃ D. 1℃~8℃
 B
【解析】试题分析:设温度为x℃,由题意得,解得3≤x≤5,故答案选B.
B
【解析】试题分析:设温度为x℃,由题意得,解得3≤x≤5,故答案选B. 不等式3x+2<2x+3的解集在数轴上表示正确的是( )
A.  B.
B. 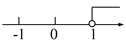 C.
C. 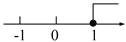 D.
D. 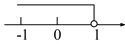
 D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D.
D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D. 如图,BE、CF是△ABC的高且相交于点P,AQ∥BC交CF延长线于点Q,若有BP=AC,CQ=AB,线段AP与AQ的关系如何?说明理由。
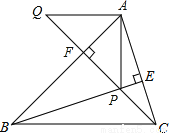
 证明见解析
【解析】试题分析:
由BE、CF是△ABC的高,易得∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,结合∠BPF=∠CPE,易得∠ABP=∠ACP,这样结合BP=AC,CQ=AB,即可由“SAS”证得△ACQ≌△PBA,从而可得AP=AQ,∠Q=∠PAF,结合∠PAF+∠APF=90°,可得:∠APF+∠Q=90°,即可得到∠QAP=90°,从而可得AQ⊥AP,由此...
证明见解析
【解析】试题分析:
由BE、CF是△ABC的高,易得∠ABP+∠BPF=90°,∠ACP+∠CPE=90°,结合∠BPF=∠CPE,易得∠ABP=∠ACP,这样结合BP=AC,CQ=AB,即可由“SAS”证得△ACQ≌△PBA,从而可得AP=AQ,∠Q=∠PAF,结合∠PAF+∠APF=90°,可得:∠APF+∠Q=90°,即可得到∠QAP=90°,从而可得AQ⊥AP,由此... 某市天然气公司在一些居民小区安装天然气管道时,采用一种鼓励居民使用天然气的收费办法,若整个小区每户都安装,收整体初装费10 000元,再对每户收费500元.某小区住户按这种收费方法全部安装天然气后,每户平均支付不足1 000元,则这个小区的住户数( )
A. 至少20户 B. 至多20户 C. 至少21户 D. 至多21户
 C
【解析】试题分析:设这个小区的住户数为x户,得共需安装费10000+500x,由每户平均支付不足1000元,则总体安装费不足1000x,列不等式求解即可.
【解析】
设这个小区的住户数为x户,
则10000+500x<1000x,解得x>20.
∵x是整数,∴这个小区的住户数至少21户.
故选C.
C
【解析】试题分析:设这个小区的住户数为x户,得共需安装费10000+500x,由每户平均支付不足1000元,则总体安装费不足1000x,列不等式求解即可.
【解析】
设这个小区的住户数为x户,
则10000+500x<1000x,解得x>20.
∵x是整数,∴这个小区的住户数至少21户.
故选C. 如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
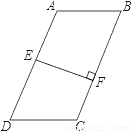
 (1)15;(2)=.
【解析】试题分析:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
(2)如图,连接EC,延长CD、BE交于点P,
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵,
∴△ABE≌△D...
(1)15;(2)=.
【解析】试题分析:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
(2)如图,连接EC,延长CD、BE交于点P,
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵,
∴△ABE≌△D... 
