题目内容
若
x2m－1－8＞5是一元一次不等式，则m的值为( )
A. 0 B. 1
C. 2 D. 3
B
【解析】根据一元一次不等式的定义得： ，故选B.
练习册系列答案
相关题目
计算
【解析】试题分析：先乘除，后加减，按照运算顺序进行运算即可.
原式 计算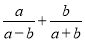
等于( )
A. 
B. 
C. 
D. 
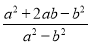
D
【解析】试题分析：原式＝
＝
＝．
故选D． 在芦山地震抢险时，太平镇部分村庄需8组战士步行运送物资，要求每组分配的人数相同，若按每组人数比预定人数多分配1人，则总数会超过100人；若按每组人数比预定人数少分配1人，则总数不够90人，那么预定每组分配的人数是（ ）
A. 10人 B. 11人 C. 12人 D. 13人
C
【解析】设预定每组分配x人，根据“按每组人数比预定人数多分配1人，总数会超过100人”得；根据“按每组人数比预定人数少分配1人，总数不够90人”得，联立得。
解得：11＜x＜12。
∵x为整数，∴x=12。故选C。 按要求解答下列各题：
(1)解不等式：3x－5＜2(2＋3x)；
(2)解不等式：2x－3≤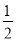
(x＋2)；
(3)解不等式： 
＜x－1，并将解集在数轴上表示出来．
(1)x＞－3 (2)x≤ (3)x＞2，画数轴略
【解析】【试题分析】（1）去括号得： 移项得： 合并同类项得： 系数化为1得：x＞－3 ；
(2) 去括号得： 移项得： 合并同类项得： 系数化为1得： x≤ ；
(3)去分母得： 移项得： ，合并得： 系数化为1得：x＞2，数轴见解析.
【试题解析】
去括号得：
移项得：
合并同类项得：
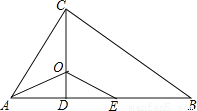
系数化为... 如图，△ABC中，∠ACB=90°，CD⊥AB于点D，AO平分∠BAC，交CD于点O，E为AB上一点，且AE=AC。
（1）求证：△AOC≌△A0E；
（2）求证：OE∥BC。
（1）证明见解析（2）证明见解析
【解析】试题分析：
（1）由AO平分∠BAC，可得∠CAO=∠EAO结合AO=AO，AE=AC即可由“SAS”证得：△AOC≌△AOE；
（2）由△AOC≌△AOE可得∠ACO=∠AEO，由∠ACB=90°，CD⊥AB于点D，易得∠ACO+∠DCB=90°，∠AEO+∠EOD=90°，从而可得∠DCB=∠DOE，即可得到：OE∥BC.
试题... 如图，AD平分∠BAC，AB=AC，那么判定△ABD≌△ACD的理由是（ ）
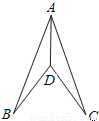
A. SSS B. SAS C. ASA D. AAS
B
【解析】∵AD平分∠BAC，
∴∠BAD=∠CAD，
又∵AB=AC，AD=AD，
∴可由“SAS”判定△ABD≌△ACD.
故选B. 小颖准备用21元钱买笔和笔记本．已知每枝笔3元，每个笔记本2.2元，她买了2个笔记本．请你帮她算一算，她还可能买几枝笔？
她还可能买5枝笔．
【解析】【试题分析】设她还可能买x只笔，根据总钱数不超过21元，列不等式求解．
【试题解析】设她还可能买x只笔，
由题意得，3x+2×2.2≤21，
解得：x≤．
答：她还可能买5枝笔． 四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：
①AD∥BC；②AD=BC；③OA=OC；④OB=OD
从中任选两个条件，能使四边形ABCD为平行四边形的选法有（ ）
A. 3种 B. 4种 C. 5种 D. 6种
B
【解析】试题分析：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形；
①③可证明△ADO≌△CBO，进而得到AD＝CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；
①④可证明△ADO≌△CBO，进而得到AD＝CB，可...