若n边形内角和为900°，则边数n= ．
7．
【解析】
试题分析：根据题意得：180（n﹣2）=900，解得：n=7．故答案为：7． 已知：如图，AB∥CD，求图形中的x的值．
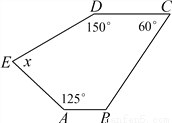
x＝85°
【解析】试题分析：先根据平行线的性质求得∠B的度数，再利用多边形的内角和定理进行求解即可.
试题解析：∵AB∥CD，∠C=60°，
∴∠B=180°-60°=120°，
∴（5-2）×180°=x+150°+125°+60°+120°，
∴x=85°． 设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（ ）
A. a＞b B. a=b C. a＜b D. b=a+180°
B
【解析】∵四边形的内角和等于a，
∴a=（4﹣2）•180°=360°．
∵五边形的外角和等于b，
∴b=360°，
∴a=b．
故选B． 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（ ）
A．108° B．90° C．72° D．60°
C．
【解析】
试题分析：设此多边形为n边形，根据题意得：180（n﹣2）=540，解得：n=5，故这个正多边形的每一个外角等于：360°÷5 =72°．故选C． 若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（ ）
A. 7 B. 10 C. 35 D. 70
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式，即可得出关于n的一元一次方程，解方程即可求出n的值，将其代入中即可得出结论．
【解析】
∵一个正n边形的每个内角为144°，
∴144n=180×（n﹣2），解得：n=10．
这个正n边形的所有对角线的条数是：==35．
故选C． 如图所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，…，照这样走下去，他第一次回到出发地A点时，一共走的路程是（ ）
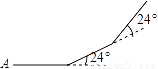
A. 140米 B. 150米 C. 160米 D. 240米
B
【解析】试题分析：已知多边形的外角和为360°，而每一个外角为24°，可得多边形的边数为360°÷24°=15，所以小明一共走了：15×10=150米．故答案选B． 一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为（ ）
A．7 B．7或8 C．8或9 D．7或8或9
D．
【解析】
试题分析：设内角和为1080°的多边形的边数是n，则（n﹣2）•180°=1080°，解得：n=8．
则原多边形的边数为7或8或9．故选D． 如图，AC是正五边形ABCDE的一条对角线，则∠ACB= ．
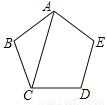
36°．
【解析】
试题分析：∵五边形ABCDE是正五边形，∴∠B=108°，AB=CB，∴∠ACB=（180°﹣108°）÷2=36°；故答案为：36°． 一个多边形的内角和是外角和的2倍，则这个多边形的边数为______．
6
【解析】∵多边形的外角和是360度，多边形的内角和是外角和的2倍，
则内角和是720度，
720÷180+2=6，
∴这个多边形是六边形，
故答案为：6． 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角.若∠A＝120°，则∠1＋∠2＋∠3＋∠4＝ .
300°
【解析】由题意得，∠5＝180°－∠EAB＝60°
，
又∵多边形的外角和为360°，
∴∠1＋∠2＋∠3＋∠4＝360°－∠5＝300°.