题目内容
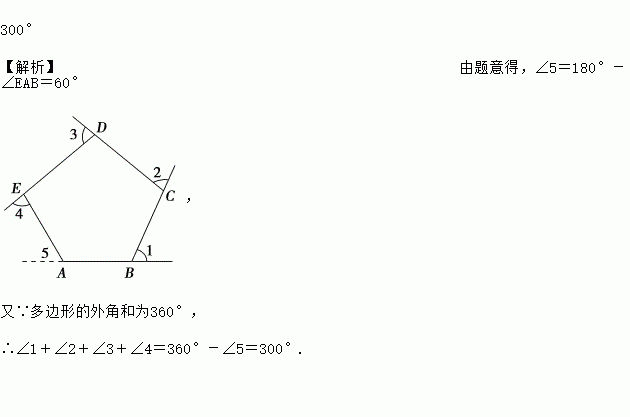
如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角.若∠A＝120°，则∠1＋∠2＋∠3＋∠4＝ .
300°
【解析】由题意得，∠5＝180°－∠EAB＝60°
，
又∵多边形的外角和为360°，
∴∠1＋∠2＋∠3＋∠4＝360°－∠5＝300°.
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
分解因式：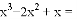
______________．
.
【解析】试题分析：==．故答案为：． 不改变分式的值，使分式的分子、分母中的首项的系数都不含 “－” 号．
①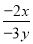
=___________； ②
=__________________；
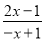③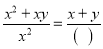
=_________；④
=______________．
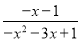【解析】①= ;
②=;
③=
④=.故答案为： (1). (2). (3). (4). 根据不等式的基本性质，把下列不等式化成x＞a或x＜a的形式：
(1)2x＞－4; (2)x－4＜－2；
(3)－2x＜1; (4) 
x＜2.
(1)x＞－2 (2)x＜2 (3)x＞－ (4)x＜4
【解析】试题分析：各不等式利用不等式的基本性质变形化为x＞a或x＜a的形式即可．
试题解析：(1)2x＞－4，
两边同时除以2，得
x>-2；
(2)x－4＜－2，
两边同时加上4，得
x<2；
(3)－2x＜1，
两边同时除以-2，得
x＞－ ；
(4) x＜2，
两... 下列变形中，不正确的是( )
A. 由x－5＞0可得x＞5
B. 由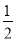
x＞0可得x＞0
C. 由－3x＞－9可得x＞3
D. 由－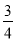
x＞1可得x＜－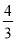
C
【解析】A、在不等式两边同加上5，不等号不变，故正确；B、在不等式的两边同时乘以2，不等号不变，故正确；C、在不等式的两边同时除以-3，不等号方向改变，故错误；D、在不等式的两边同时乘以一个负数，不等号方向改变，故正确，
故先C． 若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（ ）
A. 7 B. 10 C. 35 D. 70
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式，即可得出关于n的一元一次方程，解方程即可求出n的值，将其代入中即可得出结论．
【解析】
∵一个正n边形的每个内角为144°，
∴144n=180×（n﹣2），解得：n=10．
这个正n边形的所有对角线的条数是：==35．
故选C． 如图在△ABC中，D、E分别为AB、AC上的点，且BD＝CE，M、N分别是BE、CD的中点．过MN的直线交AB于P，交AC于Q，线段AP、AQ相等吗?为什么?
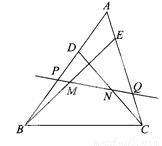
AP=AQ，理由见解析.
【解析】根据中位线定理证明MH=NH，进而证明∠HMN=∠HNM，∠HMN=∠PQA，所以△APQ为等腰三角形，即AP=AQ． 如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD=BC，∠PEF=18°，则∠PFE的度数是 度．
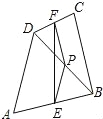
18．
【解析】
试题分析：根据中位线定理和已知，易证明△EPF是等腰三角形．∵在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，∴FP，PE分别是△CDB与△DAB的中位线，∴PF=BC，PE=AD，∵AD=BC，∴PF=PE，故△EPF是等腰三角形．∵∠PEF=18°，∴∠PEF=∠PFE=18°．故答案为：18． 下列说法中，正确的是( )
A. 两个全等三角形，一定是轴对称的
B. 两个轴对称的三角形，一定是全等的
C. 三角形的一条中线把三角形分成以中线为轴对称的两个图形
D. 三角形的一条高把三角形分成以高线为轴对称的两个图形
B
【解析】根据轴对称图形的概念对各选项分析判断即可得解．
【解析】
A. 两个全等三角形，一定是轴对称的错误，三角形全等位置上不一定关于某一直线对称，故本选项错误；
B. 两个轴对称的三角形，一定全等，正确；
C. 三角形的一条中线把三角形分成以中线为轴对称的两个图形，错误；
D. 三角形的一条高把三角形分成以高线为轴对称的两个图形，错误.
故选B.
...