题目内容
已知:如图,AB∥CD,求图形中的x的值.
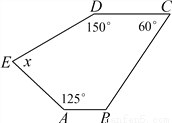
 x=85°
【解析】试题分析:先根据平行线的性质求得∠B的度数,再利用多边形的内角和定理进行求解即可.
试题解析:∵AB∥CD,∠C=60°,
∴∠B=180°-60°=120°,
∴(5-2)×180°=x+150°+125°+60°+120°,
∴x=85°.
x=85°
【解析】试题分析:先根据平行线的性质求得∠B的度数,再利用多边形的内角和定理进行求解即可.
试题解析:∵AB∥CD,∠C=60°,
∴∠B=180°-60°=120°,
∴(5-2)×180°=x+150°+125°+60°+120°,
∴x=85°.
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
下列多项式中,能用公式法分解因式的是( )
A. m2-mn B. m2+mn C. m2-n2 D. m2+n2
 C
【解析】根据平方差公式的特点: ,可知C符合题意.
故选:C.
C
【解析】根据平方差公式的特点: ,可知C符合题意.
故选:C. 当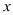 为任意实数时,下列分式中一定有意义的是( )
为任意实数时,下列分式中一定有意义的是( )
A. 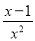 B.
B. 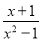 C.
C. 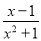 D.
D. 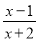
 C
【解析】A.当x=0时,x²=0,分式无意义;
B.当x=±1时,x²-1=0,分式无意义;
C.当x为任意实数时,x²+1≠0,分式有意义;
D.当x=-2时,x+2=0,分式无意义.
故选C.
C
【解析】A.当x=0时,x²=0,分式无意义;
B.当x=±1时,x²-1=0,分式无意义;
C.当x为任意实数时,x²+1≠0,分式有意义;
D.当x=-2时,x+2=0,分式无意义.
故选C. 下列不等式变形正确的是( )
A. 由a>b得ac>bc B. 由a>b得﹣2a>﹣2b
C. 由a>b得﹣a<﹣b D. 由a>b得a﹣2<b﹣2
 B
【解析】试题解析:∵a>b,
∴①c>0时,ac>bc;②c=0时,ac=bc;③c<0时,ac<bc,
∴选项A不正确;
∵a>b,
∴-2a<-2b,
∴选项B不正确;
∵a>b,
∴-a<-b,
∴选项C正确;
∵a>b,
∴a-2>b-2,
∴选项D不正确.
故选C.
B
【解析】试题解析:∵a>b,
∴①c>0时,ac>bc;②c=0时,ac=bc;③c<0时,ac<bc,
∴选项A不正确;
∵a>b,
∴-2a<-2b,
∴选项B不正确;
∵a>b,
∴-a<-b,
∴选项C正确;
∵a>b,
∴a-2>b-2,
∴选项D不正确.
故选C. 一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
 D.
【解析】
试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D.
D.
【解析】
试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D. 已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.
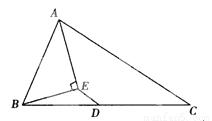
 ED=1.
【解析】延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵BE⊥AE,AE=AE,
∴△ABE≌△AFE,
∴AF=AB,BE=EF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=C...
ED=1.
【解析】延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵BE⊥AE,AE=AE,
∴△ABE≌△AFE,
∴AF=AB,BE=EF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=C... 如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.
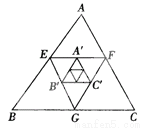
 16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长...
16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长... 工人小王4月份计划生产零件270个,前 10天平均每天生产5个,后来改进技术,提前3天超额完成任务.设小王10天之后平均每天生产零件x个,请你试着写出x所满足的关系式.
 50+(20-3)x>270
【解析】试题分析:首先设小王10天之后平均每天生产零件x个,利用4月份计划生产零件270个,改进技术后提前3天超额完成任务,进而得出不等式即可.
试题解析:设小王10天之后平均每天生产零件x个,根据题意得
50+(20-3)x>270.
50+(20-3)x>270
【解析】试题分析:首先设小王10天之后平均每天生产零件x个,利用4月份计划生产零件270个,改进技术后提前3天超额完成任务,进而得出不等式即可.
试题解析:设小王10天之后平均每天生产零件x个,根据题意得
50+(20-3)x>270. 对于下列命题:(1)关于某一直线成轴对称的两个三角形全等;(2)等腰三角形的对称轴是顶角的平分线;(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;(4)如果两个三角形全等,那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
 C
【解析】
试题分析:根据平面图形的基本概念依次分析各小题即可作出判断.
(1)关于某一直线成轴对称的两个三角形全等,(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点,均为真命题;
(2)等腰三角形的对称轴是顶角的平分线所在的直线,(4)如果两个三角形全等,它们可能是平移或旋转构成的,均为假命题;
故选C.
C
【解析】
试题分析:根据平面图形的基本概念依次分析各小题即可作出判断.
(1)关于某一直线成轴对称的两个三角形全等,(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点,均为真命题;
(2)等腰三角形的对称轴是顶角的平分线所在的直线,(4)如果两个三角形全等,它们可能是平移或旋转构成的,均为假命题;
故选C. 
