题目内容
一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
 C.
【解析】
试题分析:设此多边形为n边形,根据题意得:180(n﹣2)=540,解得:n=5,故这个正多边形的每一个外角等于:360°÷5 =72°.故选C.
C.
【解析】
试题分析:设此多边形为n边形,根据题意得:180(n﹣2)=540,解得:n=5,故这个正多边形的每一个外角等于:360°÷5 =72°.故选C.
练习册系列答案
相关题目
下列多项式不能用公式法分解因式的是( )
A. 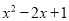 B.
B. 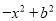 C.
C. 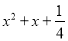 D.
D. 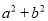
 D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D.
D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D. 当x=_____时,分式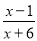 没有意义.
没有意义.
 -6
【解析】当分母x+6=0,即x=-6时,分式没有意义.故答案为:-6.
-6
【解析】当分母x+6=0,即x=-6时,分式没有意义.故答案为:-6. 因为-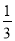 x>1,所以x____-3(填“>”或“<”),依据是__________________.
x>1,所以x____-3(填“>”或“<”),依据是__________________.
 < 不等式的基本性质3
【解析】不等式两边同时乘以-3得,x<-3,
故答案为:<,不等式的基本性质3.
< 不等式的基本性质3
【解析】不等式两边同时乘以-3得,x<-3,
故答案为:<,不等式的基本性质3. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
 6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6.
6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6. 过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是( )
A. 8 B. 9 C. 10 D. 11
 C
【解析】设多边形有n条边,
则n-2=8,解得n=10,
所以这个多边形的边数是10,
故选C.
C
【解析】设多边形有n条边,
则n-2=8,解得n=10,
所以这个多边形的边数是10,
故选C. 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是平行四边形。
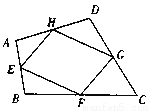
 证明见解析
【解析】试题分析:连接AC,根据三角形的中位线的性质证得线段平行且相等,从而根据平行四边形的判定(一组对边平行且相等的四边形是平行四边形)得证.
试题解析:证明:连接AC
∵E,F,G,H是四边形ABCD的中点
∴EF,HG分别是△BCA和△DCA的中位线
∴EF∥AC,HG∥AC,且EF=
∴EF∥HG, EF=HG
∴四边形EFGH是平行四...
证明见解析
【解析】试题分析:连接AC,根据三角形的中位线的性质证得线段平行且相等,从而根据平行四边形的判定(一组对边平行且相等的四边形是平行四边形)得证.
试题解析:证明:连接AC
∵E,F,G,H是四边形ABCD的中点
∴EF,HG分别是△BCA和△DCA的中位线
∴EF∥AC,HG∥AC,且EF=
∴EF∥HG, EF=HG
∴四边形EFGH是平行四... 比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
⑴32+42 2×3×4;⑵22+22 2×2×2;⑶12+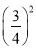 2×1×
2×1×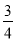 ;
;
⑷(-2) 2+52 2×(-2)×5;⑸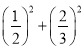
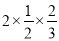
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
 (1)>(2)=(3)>(4)>(5)>; ≥2ab(当a=b时取等号).
【解析】试题分析:分别根据有理数的乘方法则求出各数的值,再根据有理数比较大小的法则比较出各数的大小,并总结出规律.
试题解析:(1)∵32+42=25,2×3×4=24,
∴32+42>2×3×4;
(2)∵22+22=8,2×2×2=8,
∴22+22=2×2×2;
(3)∵12+()...
(1)>(2)=(3)>(4)>(5)>; ≥2ab(当a=b时取等号).
【解析】试题分析:分别根据有理数的乘方法则求出各数的值,再根据有理数比较大小的法则比较出各数的大小,并总结出规律.
试题解析:(1)∵32+42=25,2×3×4=24,
∴32+42>2×3×4;
(2)∵22+22=8,2×2×2=8,
∴22+22=2×2×2;
(3)∵12+()... 下列图案中,不能用折叠剪纸方法得到的是( )




A. B. C. D.
 C
【解析】根据轴对称图形的定义即可解答.
【解析】
由给出的图案,结合轴对称的性质,可知C是旋转一定的角度后与原来的图案对称的,不是一个轴对称图形,故选C.
C
【解析】根据轴对称图形的定义即可解答.
【解析】
由给出的图案,结合轴对称的性质,可知C是旋转一定的角度后与原来的图案对称的,不是一个轴对称图形,故选C. 
