题目内容
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
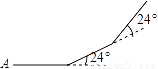
A. 140米 B. 150米 C. 160米 D. 240米
 B
【解析】试题分析:已知多边形的外角和为360°,而每一个外角为24°,可得多边形的边数为360°÷24°=15,所以小明一共走了:15×10=150米.故答案选B.
B
【解析】试题分析:已知多边形的外角和为360°,而每一个外角为24°,可得多边形的边数为360°÷24°=15,所以小明一共走了:15×10=150米.故答案选B.
练习册系列答案
相关题目
下列能用平方差公式分解因式的是( )
A. 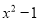 B.
B. 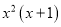 C.
C. 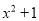 D.
D. 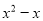
 A
【解析】根据平方差公式: ,A选项: ,可知能用平方差公式进行因式分解.
故选:A.
A
【解析】根据平方差公式: ,A选项: ,可知能用平方差公式进行因式分解.
故选:A. 化简分式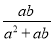 的结果为_____.
的结果为_____.
 【解析】= ,故答案为: .
【解析】= ,故答案为: . 把不等式2x>3-x化为x>a或x<a的形式是( )
A. x>3 B. x<3
C. x>1 D. x<1
 C
【解析】2x>3-x,
两边同时加上x,
2x+x>3,
3x>3,
两边同时除以3得
x>1,
故选C.
C
【解析】2x>3-x,
两边同时加上x,
2x+x>3,
3x>3,
两边同时除以3得
x>1,
故选C. 已知一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
 7
【解析】试题分析:多边形的外角和是360°,根据多边形的内角和比它的外角和的3倍少180°,即可得到多边形的内角和的度数.根据多边形的内角和定理即可求得多边形的边数
试题解析:【解析】
设多边形的边数为n,依题意得
(n-2).180°= 3×360°-180°
解得n=7
答:这个多边形的边数是7
7
【解析】试题分析:多边形的外角和是360°,根据多边形的内角和比它的外角和的3倍少180°,即可得到多边形的内角和的度数.根据多边形的内角和定理即可求得多边形的边数
试题解析:【解析】
设多边形的边数为n,依题意得
(n-2).180°= 3×360°-180°
解得n=7
答:这个多边形的边数是7 若n边形内角和为900°,则边数n= .
 7.
【解析】
试题分析:根据题意得:180(n﹣2)=900,解得:n=7.故答案为:7.
7.
【解析】
试题分析:根据题意得:180(n﹣2)=900,解得:n=7.故答案为:7. 已知:如图,E为□ABCD中DC边的延长线上的一点,且CE=DC,连结AE分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB=2OF.
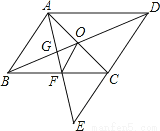
 证明见解析.
【解析】
试题分析:先证明△ABF≌△ECF得BF=FC,再利用三角形中位线定理即可解决问题.
试题解析:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AO=OC,
∵CD=CE,
∴AB=CE,∠BAF=∠CEF,
在△ABF和△ECF中,
,
∴△ABF≌△ECF,
∴BF=FC,
∵AO=OC,
...
证明见解析.
【解析】
试题分析:先证明△ABF≌△ECF得BF=FC,再利用三角形中位线定理即可解决问题.
试题解析:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AO=OC,
∵CD=CE,
∴AB=CE,∠BAF=∠CEF,
在△ABF和△ECF中,
,
∴△ABF≌△ECF,
∴BF=FC,
∵AO=OC,
... 如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE= .
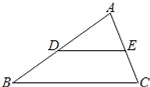
 4
【解析】试题分析:已知D、E分别是边AB、AC的中点,BC=8,根据三角形的中位线定理得到DE=BC=4.
4
【解析】试题分析:已知D、E分别是边AB、AC的中点,BC=8,根据三角形的中位线定理得到DE=BC=4. 下列右侧四幅图中,平行移动到位置M后能与N成轴对称的是( )


A. 图1 B. 图2 C. 图3 D. 图4
 C
【解析】根据平移的性质即可解答.
解答:要想平行移动到位置M后能与N成轴对称,则一定是以M、N的公共边所在直线为对称轴,故选C.
C
【解析】根据平移的性质即可解答.
解答:要想平行移动到位置M后能与N成轴对称,则一定是以M、N的公共边所在直线为对称轴,故选C. 
