已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．
7
【解析】试题分析：多边形的外角和是360°，根据多边形的内角和比它的外角和的3倍少180°，即可得到多边形的内角和的度数．根据多边形的内角和定理即可求得多边形的边数
试题解析：【解析】
设多边形的边数为n，依题意得
（n－2）．180°＝ 3×360°－180°
解得n＝7
答：这个多边形的边数是7 在五边形ABCDE中，∠A＋∠B＝240°，∠C＝∠D＝∠E＝2∠B.求∠B的度数．
50°
【解析】试题分析：首先求得五边形ABCDE的内角和，设∠B=x°，即可利用x表示其它角的度数，根据多边形的内角和定理即可列方程，从而求得∠B的度数．
试题解析：五边形ABCDE的内角和是（5-2）×180°=540°，
设∠B=x°，则∠C=∠D=∠E=2∠B=2x°，
∵∠A+∠B=240°
∴∠A=240-x°
∵∠A+∠B+∠C+∠D+∠E=540... 若x＞y，则下列式子中错误的是( )
A. x－3＞y－3 B. x＋3＞y＋3
C. －3x＞－3y D.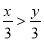 
C
【解析】试题分析：A、不等式的两边都减3，不等号的方向不变，故A正确；
B、不等式的两边都加3，不等号方向不变，故B正确；
C、不等式的两边都乘-3，不等号的方向改变，故C错误；
D、不等式的两边都除以3，不等号的方向改变，故D正确；
故选C． 下列不等式变形正确的是（ ）
A. 由a＞b得ac＞bc B. 由a＞b得﹣2a＞﹣2b
C. 由a＞b得﹣a＜﹣b D. 由a＞b得a﹣2＜b﹣2
B
【解析】试题解析：∵a＞b，
∴①c＞0时，ac＞bc；②c=0时，ac=bc；③c＜0时，ac＜bc，
∴选项A不正确；
∵a＞b，
∴-2a＜-2b，
∴选项B不正确；
∵a＞b，
∴-a＜-b，
∴选项C正确；
∵a＞b，
∴a-2＞b-2，
∴选项D不正确．
故选C． 下列变形中，不正确的是( )
A. 由x－5＞0可得x＞5
B. 由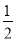
x＞0可得x＞0
C. 由－3x＞－9可得x＞3
D. 由－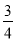
x＞1可得x＜－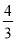
C
【解析】A、在不等式两边同加上5，不等号不变，故正确；B、在不等式的两边同时乘以2，不等号不变，故正确；C、在不等式的两边同时除以-3，不等号方向改变，故错误；D、在不等式的两边同时乘以一个负数，不等号方向改变，故正确，
故先C． 因为－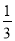
x＞1，所以x____－3(填“＞”或“＜”)，依据是__________________.
< 不等式的基本性质3
【解析】不等式两边同时乘以-3得，x＜-3，
故答案为：<，不等式的基本性质3． 用不等号填空：(1)若a＞b，则ac2___bc2；(2)若a＞b，则3－2a___3－2b.
≥ <
【解析】（1）当c=0时，ac2=bc2，
当c≠0时， ac2＞bc2，
故答案为：≥；
（2）因为a>b，由不等式的性质3有：－2a<－2b，再由不等式的性质1得，3－2a＞3－2b，故答案为：<. 把不等式2x＞3－x化为x＞a或x＜a的形式是( )
A. x＞3 B. x＜3
C. x＞1 D. x＜1
C
【解析】2x＞3－x，
两边同时加上x，
2x+x>3，
3x>3，
两边同时除以3得
x>1，
故选C. 小明的作业本上有四道利用不等式的性质，将不等式化为x＞a或x＜a的作业题：①由x＋7＞8解得x＞1；②由x＜2x＋3解得x＜3；③由3x－1＞x＋7解得x＞4；④由－3x＞－6解得x＜－2.其中正确的有( )
A. 1题 B. 2题
C. 3题 D. 4题
B
【解析】①不等式的两边都减7，得x>1，故①正确；
②不等式两边都减（x+3），得x>-3，故②错误；
③不等式的两边都加（1-x），得2x>8，不等式的两边都除以2，得x>4，故③正确；
④不等式的两边都除以-3，得x<2，故④错误，
所以正确的有2题，
故选B． 根据不等式的基本性质，可将“mx＜2”化为“x＞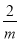
”，则m的取值范围是_____.
m＜0
【解析】因为mx＜2化为x＞，
根据不等式的基本性质3得：m＜0，
故答案为：m＜0．