题目内容
下列不等式变形正确的是( )
A. 由a>b得ac>bc B. 由a>b得﹣2a>﹣2b
C. 由a>b得﹣a<﹣b D. 由a>b得a﹣2<b﹣2
 B
【解析】试题解析:∵a>b,
∴①c>0时,ac>bc;②c=0时,ac=bc;③c<0时,ac<bc,
∴选项A不正确;
∵a>b,
∴-2a<-2b,
∴选项B不正确;
∵a>b,
∴-a<-b,
∴选项C正确;
∵a>b,
∴a-2>b-2,
∴选项D不正确.
故选C.
B
【解析】试题解析:∵a>b,
∴①c>0时,ac>bc;②c=0时,ac=bc;③c<0时,ac<bc,
∴选项A不正确;
∵a>b,
∴-2a<-2b,
∴选项B不正确;
∵a>b,
∴-a<-b,
∴选项C正确;
∵a>b,
∴a-2>b-2,
∴选项D不正确.
故选C.
练习册系列答案
相关题目
______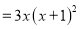
 【解析】根据因式分解与整式乘法的互逆性,可知直接进行乘法计算为: =.
故答案为: .
【解析】根据因式分解与整式乘法的互逆性,可知直接进行乘法计算为: =.
故答案为: . 先化简,后求值: 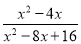 ,其中x=5.
,其中x=5.
 5
【解析】原式=,
把x=5代入得,原式=5.
5
【解析】原式=,
把x=5代入得,原式=5. 下列分式中,当x=1时,有意义的是( )
①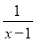 ;②
;②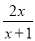 ;③
;③ ;④
;④ .
.
A. ①③ B. ①②③ C. ②③ D. ②④
 D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
综上所述,当x=1时,分式、有意义.故选D.
D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
综上所述,当x=1时,分式、有意义.故选D. 小明的作业本上有四道利用不等式的性质,将不等式化为x>a或x<a的作业题:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A. 1题 B. 2题
C. 3题 D. 4题
 B
【解析】①不等式的两边都减7,得x>1,故①正确;
②不等式两边都减(x+3),得x>-3,故②错误;
③不等式的两边都加(1-x),得2x>8,不等式的两边都除以2,得x>4,故③正确;
④不等式的两边都除以-3,得x<2,故④错误,
所以正确的有2题,
故选B.
B
【解析】①不等式的两边都减7,得x>1,故①正确;
②不等式两边都减(x+3),得x>-3,故②错误;
③不等式的两边都加(1-x),得2x>8,不等式的两边都除以2,得x>4,故③正确;
④不等式的两边都除以-3,得x<2,故④错误,
所以正确的有2题,
故选B. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
 6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6.
6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6. 已知:如图,AB∥CD,求图形中的x的值.
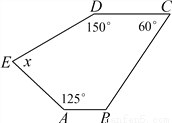
 x=85°
【解析】试题分析:先根据平行线的性质求得∠B的度数,再利用多边形的内角和定理进行求解即可.
试题解析:∵AB∥CD,∠C=60°,
∴∠B=180°-60°=120°,
∴(5-2)×180°=x+150°+125°+60°+120°,
∴x=85°.
x=85°
【解析】试题分析:先根据平行线的性质求得∠B的度数,再利用多边形的内角和定理进行求解即可.
试题解析:∵AB∥CD,∠C=60°,
∴∠B=180°-60°=120°,
∴(5-2)×180°=x+150°+125°+60°+120°,
∴x=85°. 如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).
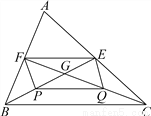
 (1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是...
(1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是... 若一个三角形是轴对称图形,则这个三角形一定是( )
A. 等边三角形 B. 不等边三角形 C. 等腰三角形 D. 等腰直角三角形
 C
【解析】根据轴对称图形的性质即可得出答案.
A等边三角形一定是轴对称图形,但轴对称三角形不一定是等边三角形;
B不等边三角形一定不是轴对称图形;
C等腰三角形一定是轴对称三角形;
D等腰直角三角形一定是轴对称图形,但是轴对称三角形不一定是等腰直角三角形.故选C.
C
【解析】根据轴对称图形的性质即可得出答案.
A等边三角形一定是轴对称图形,但轴对称三角形不一定是等边三角形;
B不等边三角形一定不是轴对称图形;
C等腰三角形一定是轴对称三角形;
D等腰直角三角形一定是轴对称图形,但是轴对称三角形不一定是等腰直角三角形.故选C. 
