题目内容
在五边形ABCDE中,∠A+∠B=240°,∠C=∠D=∠E=2∠B.求∠B的度数.
 50°
【解析】试题分析:首先求得五边形ABCDE的内角和,设∠B=x°,即可利用x表示其它角的度数,根据多边形的内角和定理即可列方程,从而求得∠B的度数.
试题解析:五边形ABCDE的内角和是(5-2)×180°=540°,
设∠B=x°,则∠C=∠D=∠E=2∠B=2x°,
∵∠A+∠B=240°
∴∠A=240-x°
∵∠A+∠B+∠C+∠D+∠E=540...
50°
【解析】试题分析:首先求得五边形ABCDE的内角和,设∠B=x°,即可利用x表示其它角的度数,根据多边形的内角和定理即可列方程,从而求得∠B的度数.
试题解析:五边形ABCDE的内角和是(5-2)×180°=540°,
设∠B=x°,则∠C=∠D=∠E=2∠B=2x°,
∵∠A+∠B=240°
∴∠A=240-x°
∵∠A+∠B+∠C+∠D+∠E=540...
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
将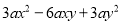 分解因式是___________
分解因式是___________
 【解析】根据题意,先提公因式,再根据平方差公式分解即可得: .
故答案为: .
【解析】根据题意,先提公因式,再根据平方差公式分解即可得: .
故答案为: . 化简下列各分式.
(1)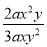 ; (2)
; (2)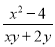 .
.
 (1) (2) .
【解析】(1) =;
(2)原式=.
故答案为:(1) (2) .
(1) (2) .
【解析】(1) =;
(2)原式=.
故答案为:(1) (2) . 某商贩去菜摊买西红柿,他上午买了30斤,价格为每斤x元;下午,他又买了20斤,价格为每斤y元,后来他以每斤 元的价格卖完后.发现自己赔了钱,你知道是什么原因吗?
元的价格卖完后.发现自己赔了钱,你知道是什么原因吗?
 见解析
【解析】试题分析:题目中的不等关系是:买黄瓜每斤平均价>卖黄瓜每斤平均价,据此列不等式进行求解即可.
试题解析:根据题意得,他买西红柿每斤平均价是元,
以每斤元的价格卖完后,结果发现自己赔了钱,
则>
解之得,x>y,
所以赔钱的原因是x>y.
即此商贩上午所买的西红柿的单价高于下午的单价,所以赔了钱.
见解析
【解析】试题分析:题目中的不等关系是:买黄瓜每斤平均价>卖黄瓜每斤平均价,据此列不等式进行求解即可.
试题解析:根据题意得,他买西红柿每斤平均价是元,
以每斤元的价格卖完后,结果发现自己赔了钱,
则>
解之得,x>y,
所以赔钱的原因是x>y.
即此商贩上午所买的西红柿的单价高于下午的单价,所以赔了钱. 用不等号填空:(1)若a>b,则ac2___bc2;(2)若a>b,则3-2a___3-2b.
 ≥ <
【解析】(1)当c=0时,ac2=bc2,
当c≠0时, ac2>bc2,
故答案为:≥;
(2)因为a>b,由不等式的性质3有:-2a<-2b,再由不等式的性质1得,3-2a>3-2b,故答案为:<.
≥ <
【解析】(1)当c=0时,ac2=bc2,
当c≠0时, ac2>bc2,
故答案为:≥;
(2)因为a>b,由不等式的性质3有:-2a<-2b,再由不等式的性质1得,3-2a>3-2b,故答案为:<. 一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
 D.
【解析】
试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D.
D.
【解析】
试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D. 六边形的内角和是( )
A.540° B.720° C.900° D.360°
 B.
【解析】
试题分析:根据多边形的内角和公式可得六边形的内角和是(6﹣2)×180°=720°,故答案选B.
B.
【解析】
试题分析:根据多边形的内角和公式可得六边形的内角和是(6﹣2)×180°=720°,故答案选B. 如图,已知△ABC中,D为AB的中点.
(1)请用尺规作图法作边AC的中点E,并连接DE(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若DE=4,求BC的长.
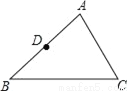
 (1)作图见解析;(2)BC=8.
【解析】试题分析:(1)作线段的垂直平分线即可.
(2)根据三角形中位线定理即可解决.
试题解析:(1)作线段的垂直平分线交于,点就是所求的点.
(2)分别为的中点,
(1)作图见解析;(2)BC=8.
【解析】试题分析:(1)作线段的垂直平分线即可.
(2)根据三角形中位线定理即可解决.
试题解析:(1)作线段的垂直平分线交于,点就是所求的点.
(2)分别为的中点, 如图,△ABC和△A′B′C′关于直线l对称,下列结论中:
①△ABC≌△A′B′C′;
②∠BAC′=∠B′AC;
③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
正确的有( )
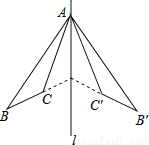
A. 4个 B. 3个 C. 2个 D. 1个
 B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称,
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故...
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称,
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故... 
