题目内容
把不等式2x＞3－x化为x＞a或x＜a的形式是( )
A. x＞3 B. x＜3
C. x＞1 D. x＜1
C
【解析】2x＞3－x，
两边同时加上x，
2x+x>3，
3x>3，
两边同时除以3得
x>1，
故选C.
练习册系列答案
相关题目
分解因式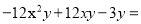
___________
【解析】根据因式分解的方法，先提公因式-3y，再根据完全平方公式分解因式为： .
故答案为： . 如图，AB=AC，添加下列条件，能用SAS判断△ABE≌△ACD的是（ ）
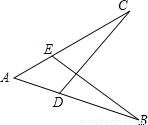
A. ∠B=∠C B. ∠AEB=∠ADC C. AE=AD D. BE=DC
C
【解析】∵AB=AC （已知），∠A=∠A（公共角），
∴只需要AE=AD，
∴△ABE≌△ACD，
故选：C. 已知有理式：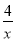 
、
、
、
、
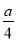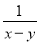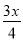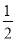x2、
＋4，其中分式有 （ ）
A. 2个 B. 3个 C. 4个 D. 5个
B
【解析】、、、x2的分母中均不含有字母,因此它们是整式,而不是分式.
、、、＋4的分母中含有字母,因此是分式.
所以B选项是正确的. 某商店先在广州以每件15元的价格购进某种商品10件，后来又到深圳以每件12.5元的价格购进同种商品40件，如果商店销售这些商品时，每件定价为x元，则会获得不少于12%的利润，用不等式表示以上问题中的不等关系，并把这个不等式变形为“x≥a”或“x≤a”的形式．
x≥14.56.
【解析】试题分析：关系式为：总售价-总进价＞总进价×12%，把相关数值代入化简即可.
试题解析：由题意得
(10＋40)x－(15×10＋12.5×40)≥(15×10＋12.5×40)×12%，
∴x≥14.56. 若x＞y，则下列式子中错误的是( )
A. x－3＞y－3 B. x＋3＞y＋3
C. －3x＞－3y D.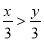 
C
【解析】试题分析：A、不等式的两边都减3，不等号的方向不变，故A正确；
B、不等式的两边都加3，不等号方向不变，故B正确；
C、不等式的两边都乘-3，不等号的方向改变，故C错误；
D、不等式的两边都除以3，不等号的方向改变，故D正确；
故选C． 如图所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，…，照这样走下去，他第一次回到出发地A点时，一共走的路程是（ ）
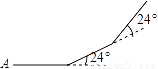
A. 140米 B. 150米 C. 160米 D. 240米
B
【解析】试题分析：已知多边形的外角和为360°，而每一个外角为24°，可得多边形的边数为360°÷24°=15，所以小明一共走了：15×10=150米．故答案选B． (1)三角形的中位线的定义：连结三角形两边____________叫做三角形的中位线．
(2)三角形的中位线定理是三角形的中位线________第三边，并且等于___________．
(1)中点的线段; (2)平行于三角形的 第三边的一半
【解析】(1)三角形的中位线的定义：连结三角形两边中点的线段叫做三角形的中位线，
故答案为：中点的线段；
(2)三角形的中位线定理是三角形的中位线平行于三角形的第三边，并且等于第三边的一半，
故答案为：平行于三角形的，第三边的一半. 如图，△ABC中，∠ A=500，∠C=700，BD、BE三等分∠ABC，将△BCE沿BE对折，点C落在C’处，则∠1=_________；
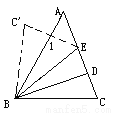
90°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1的度数.
【解析】
∵∠ A=500，∠C=700，
∴∠ABC =60°，
∵BD、BE三等分∠ABC，
∴∠ABE =∠EBD =∠DBC =20°，
∴∠EBC =∠EBD +∠DBC =40°，
由翻折得∠C’BE=∠EBC =40°， ∠C’ =...