题目内容
因为－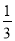
x＞1，所以x____－3(填“＞”或“＜”)，依据是__________________.
< 不等式的基本性质3
【解析】不等式两边同时乘以-3得，x＜-3，
故答案为：<，不等式的基本性质3．
练习册系列答案
相关题目
因式分解: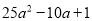 
=______________
【解析】根据完全平方公式进行因式分解为： =.
故答案为： . 已知x2＋3x－1=0，求x－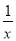
和x2＋
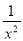的值．
－3,11
【解析】分析：首先将3x移项,再方程两边同除以x得出即可,再利用,方程两边同时平方求出即可.
本题解析：
因为 ,
所以 ,
将上式子两边同时除以x(x≠0),
所以 ,
,
,
则.故答案为：-3，,11. 若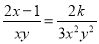
，则k的值为 （ ）
A. 3x2y2(2x-1) B. 
xy(2x-1) C. 
xy2(2x-1) D. xy2(2x-1)
B
【解析】∵, ∴2k=,∴k= (6x²y-3xy)= xy(2x-1).故选B. 已知x满足－5x＋5＜－10，则x的范围是_____.
x＞3
【解析】－5x＋5＜－10，
两边同时减去5，得
-5x<-10-5，
两边同时除以-5，得
x>3，
故答案为：x>3. 已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．
7
【解析】试题分析：多边形的外角和是360°，根据多边形的内角和比它的外角和的3倍少180°，即可得到多边形的内角和的度数．根据多边形的内角和定理即可求得多边形的边数
试题解析：【解析】
设多边形的边数为n，依题意得
（n－2）．180°＝ 3×360°－180°
解得n＝7
答：这个多边形的边数是7 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（ ）
A．108° B．90° C．72° D．60°
C．
【解析】
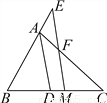
试题分析：设此多边形为n边形，根据题意得：180（n﹣2）=540，解得：n=5，故这个正多边形的每一个外角等于：360°÷5 =72°．故选C． 如图，已知△ABC，AD平分∠BAC交BC于点D，BC的中点为M，ME∥AD，交BA的延长线于点E，交AC于点F.
(1)求证：AE＝AF；
(2)求证：BE＝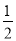
(AB＋AC)．
（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据角平分线的性质及平行线的性质易∠AEF=∠AFE，即可得AE=AF；（2）作CG∥EM，交BA的延长线于G，已知AC=AG，根据三角形中位线定理的推论证明BE=EG，再利用三角形的中位线定理即可证得结论．
试题解析：
（1）∵DA平分∠BAC，
∴∠BAD=∠CAD，
∵AD∥EM，
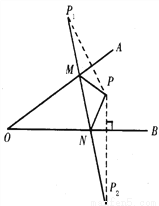
∴∠BAD=... 如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为_______.
5cm
【解析】∵P、P1,P、P2关于OA、OB对称，
∴PM=P1M,PN=P2N，
∴△PMN的周长=P1P2，
∴△PMN的周长是5 cm.