如图,MN与PQ相交于点O,MO=OP,QO=ON,∠M=65°,∠Q=30°,则∠P=____,∠N=___.
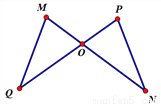
 65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30°
65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30° 如图,已知AB=AC=12 cm,AE=AF=7 cm,CE=10 cm,△ABF的周长是_________.
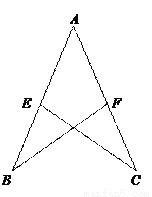
 29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm.
29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm. 如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 (答案不唯一,只需填一个)
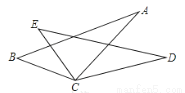
 AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定. 在如图所示的2×2方格中,连接AB、AC,则∠1+∠2=_____度.
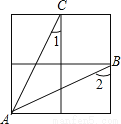
 90°
【解析】在△ACM和△BAN中,AN=CM,∠AMC=∠BNA,CM=AN
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.故答案为:90°.
90°
【解析】在△ACM和△BAN中,AN=CM,∠AMC=∠BNA,CM=AN
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.故答案为:90°. 已知:如图,点C为AB中点,CD=BE,CD∥BE.求证:△ACD≌△CBE.
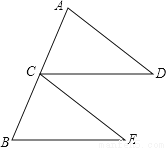
 证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS)
证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS) 如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
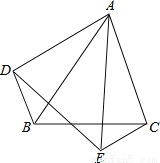
 证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等.
证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等. 已知:如图,AD是△ABC的高,E是AD上一点,BE的延长线交AC于点F,BE=AC,DE=DC,BE和AC垂直吗?说明理由.
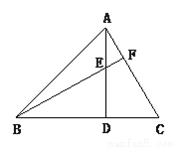
 BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE...
BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE... 如图,已知AB=AC,E,D分别是AB,AC的中点,且AF⊥BD交BD的延长线于F,AG⊥CE交CE的延长线于G,试判断AF和AG的关系是否相等,并说明理由.
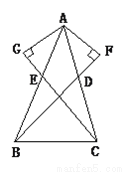
 AF=AG
【解析】试题分析:先由SAS证得△ABD≌△ACE,由全等三角形对应边相等得∠ABD=∠ACE,由AAS证得△ABF≌△ACG,即可证得AF=AG.
试题解析:
∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD=∠ACE,
在△ABF和△ACG中,
...
AF=AG
【解析】试题分析:先由SAS证得△ABD≌△ACE,由全等三角形对应边相等得∠ABD=∠ACE,由AAS证得△ABF≌△ACG,即可证得AF=AG.
试题解析:
∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD=∠ACE,
在△ABF和△ACG中,
... 如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
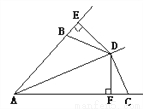
 见解析
【解析】试题分析:首先由角平分线的性质可得DE=DF,然后根据HL可证Rt△BDE≌Rt△CDF,即可证明BE=CF.
试题解析:相等.
理由是:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
见解析
【解析】试题分析:首先由角平分线的性质可得DE=DF,然后根据HL可证Rt△BDE≌Rt△CDF,即可证明BE=CF.
试题解析:相等.
理由是:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF. 下列多项式能用完全平方公式分解因式的是( )
A. 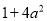 B.
B. 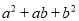 C.
C. 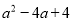 D.
D. 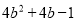
 C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C.
C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C.