题目内容
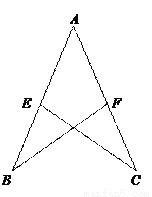
如图,已知AB=AC=12 cm,AE=AF=7 cm,CE=10 cm,△ABF的周长是_________.
 29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm.
29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm.
已知∠AOB及其内部一点P,试讨论以下问题的解答:
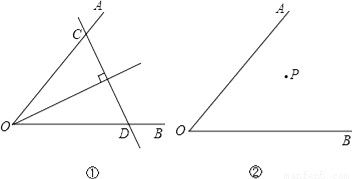
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
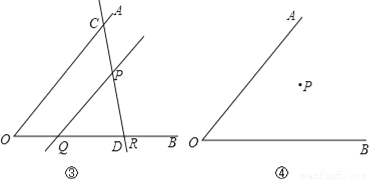
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.
 (1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:【解析】
(1)能.
...
(1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:【解析】
(1)能.
... 在公式法分解因式中,有一种公式a3+b3=(a+b)(a2-ab+b2)叫立方和公式,请用它把x3+8分解因式
 (x+2)·(x2-2x+4)
【解析】试题分析:根据所给公式,将x3+8先变形为x3+23,然后套用公式,进行分解即可.
试题解析:x3+8=x3+23=(x+2)·(x2-2x+4)
(x+2)·(x2-2x+4)
【解析】试题分析:根据所给公式,将x3+8先变形为x3+23,然后套用公式,进行分解即可.
试题解析:x3+8=x3+23=(x+2)·(x2-2x+4) 下列多项式不能用公式法分解因式的是( )
A. 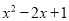 B.
B. 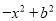 C.
C. 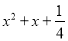 D.
D. 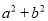
 D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D.
D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D. 已知:如图,AD是△ABC的高,E是AD上一点,BE的延长线交AC于点F,BE=AC,DE=DC,BE和AC垂直吗?说明理由.
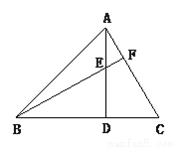
 BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE...
BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE... 已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )
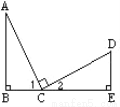
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△CED D. ∠1=∠2
 D
【解析】∵AC⊥CD,
∴∠1+∠2=90°,
∵∠B=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
在△ABC和△CED中,
,
∴△ABC≌△CED(AAS),
故B、C选项正确;
∵∠2+∠D=90°,
∴∠A+∠D=90°,
故A选项正确;
∵AC⊥CD,
∴∠ACD=90°,
∠1+∠2=...
D
【解析】∵AC⊥CD,
∴∠1+∠2=90°,
∵∠B=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
在△ABC和△CED中,
,
∴△ABC≌△CED(AAS),
故B、C选项正确;
∵∠2+∠D=90°,
∴∠A+∠D=90°,
故A选项正确;
∵AC⊥CD,
∴∠ACD=90°,
∠1+∠2=... 如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
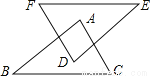
A. 40° B. 50° C. 60° D. 70°
 D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D .
D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D . 当x=_____时,分式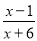 没有意义.
没有意义.
 -6
【解析】当分母x+6=0,即x=-6时,分式没有意义.故答案为:-6.
-6
【解析】当分母x+6=0,即x=-6时,分式没有意义.故答案为:-6. 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是平行四边形。
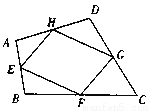
 证明见解析
【解析】试题分析:连接AC,根据三角形的中位线的性质证得线段平行且相等,从而根据平行四边形的判定(一组对边平行且相等的四边形是平行四边形)得证.
试题解析:证明:连接AC
∵E,F,G,H是四边形ABCD的中点
∴EF,HG分别是△BCA和△DCA的中位线
∴EF∥AC,HG∥AC,且EF=
∴EF∥HG, EF=HG
∴四边形EFGH是平行四...
证明见解析
【解析】试题分析:连接AC,根据三角形的中位线的性质证得线段平行且相等,从而根据平行四边形的判定(一组对边平行且相等的四边形是平行四边形)得证.
试题解析:证明:连接AC
∵E,F,G,H是四边形ABCD的中点
∴EF,HG分别是△BCA和△DCA的中位线
∴EF∥AC,HG∥AC,且EF=
∴EF∥HG, EF=HG
∴四边形EFGH是平行四... 
