题目内容
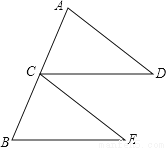
已知:如图,点C为AB中点,CD=BE,CD∥BE.求证:△ACD≌△CBE.
 证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS)
证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS)
练习册系列答案
相关题目
一元一次不等式2(x+1)≥4的解集在数轴上表示为( )
A.  B.
B.  C.
C. 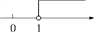 D.
D. 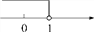
 A
【解析】试题分析:首先进行去括号可得:2x+2≥4,则2x≥2,解得:x≥1,在数轴上就是在1的右边,且表示1的点需要用实心点来表示.
A
【解析】试题分析:首先进行去括号可得:2x+2≥4,则2x≥2,解得:x≥1,在数轴上就是在1的右边,且表示1的点需要用实心点来表示. 已知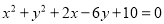 ,则
,则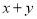 的值?
的值?
 2
【解析】试题分析:根据拆分法,构成完全平方公式,然后分解因式为非负数的和的形式,然后求解即可.
试题解析:因为,所以根据平方的非负性可以得到x=-1,y=3,则.
2
【解析】试题分析:根据拆分法,构成完全平方公式,然后分解因式为非负数的和的形式,然后求解即可.
试题解析:因为,所以根据平方的非负性可以得到x=-1,y=3,则. 把多项式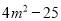 分解因式正确的是( )
分解因式正确的是( )
A. 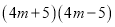 B.
B. 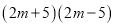
C. 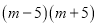 D.
D. 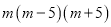
 B
【解析】利用公式法分解因式的要点,根据平方差公式: ,分解因式为: .
故选:B.
B
【解析】利用公式法分解因式的要点,根据平方差公式: ,分解因式为: .
故选:B. 下列多项式能用完全平方公式分解因式的是( )
A. 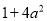 B.
B. 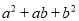 C.
C. 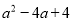 D.
D. 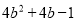
 C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C.
C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C. 已知:如图,点A,E,F,D在同一条直线上,AE=DF,AB=CD,BF⊥AD,CE⊥AD,垂足分别为F,E,则△ABF≌△DCE的依据是( )
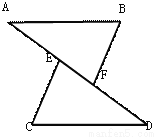
A. SSS B. SAS C. ASA D. HL
 D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D.
D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D. 下列说法正确的是( )
A. 两个周长相等的长方形全等 B. 两个周长相等的三角形全等
C. 两个面积相等的长方形全等 D. 两个周长相等的圆全等
 D
【解析】A.长方形周长相等,但面积、长、宽不一定相等,错;
B.三角形周长相等,但不一定对应边完全相等,错;
C.长方形面积相等,但长、宽不一定相等,错;
D.圆的周长相等,就可知道半径相等,两圆可完全重合,正确。
故选:D.
D
【解析】A.长方形周长相等,但面积、长、宽不一定相等,错;
B.三角形周长相等,但不一定对应边完全相等,错;
C.长方形面积相等,但长、宽不一定相等,错;
D.圆的周长相等,就可知道半径相等,两圆可完全重合,正确。
故选:D. .填空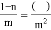 .
.
 m-mn
【解析】由分母可知:左边分式的分子与分母都乘以m可得:.故答案为:m-mn.
m-mn
【解析】由分母可知:左边分式的分子与分母都乘以m可得:.故答案为:m-mn. 已知,如图,在?ABCD中,E是CD的中点,F是AE的中点,FC与BE交于点G.求证:GF=GC.
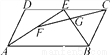
 证明见解析
【解析】试题分析:取BE的中点H,连接FH,CH,利用三角形中位线定理求FH=AB,利用平行四边形判断定理可得到CEFH是平行四边形,所以GF=GC.
试题解析:
取BE的中点H,连接FH,CH,∵F是AE的中点,∴FH∥AB,FH=AB.∵CD∥AB,CD=AB,CE=CD,∴CE∥FH,且CE=FH.∴四边形CEFH是平行四边形.∴GF=GC.
证明见解析
【解析】试题分析:取BE的中点H,连接FH,CH,利用三角形中位线定理求FH=AB,利用平行四边形判断定理可得到CEFH是平行四边形,所以GF=GC.
试题解析:
取BE的中点H,连接FH,CH,∵F是AE的中点,∴FH∥AB,FH=AB.∵CD∥AB,CD=AB,CE=CD,∴CE∥FH,且CE=FH.∴四边形CEFH是平行四边形.∴GF=GC. 
