题目内容
如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
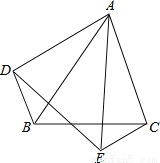
 证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等.
证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果(m+3)x>2m+6的解集为x<2,则m的取值范围是( )
A. m<0 B. m<-3 C. m>-3 D. m是任意实数
 B
【解析】由含有m的不等式(m+3)x>2m+6的解集为:x<2,根据不等式的基本性质3,可知m+3<0,解得m<-3.
故选:B.
B
【解析】由含有m的不等式(m+3)x>2m+6的解集为:x<2,根据不等式的基本性质3,可知m+3<0,解得m<-3.
故选:B. 多项式-6ab2+18a2b2-12a3b2c的公因式是( )
A.-6ab2c B.-ab2 C.-6ab2 D.-6a3b2c
 C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C.
C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C. 下列式子分解因式能用公式法分解因式的是 ( ).
A. 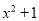 B.
B. 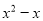 C.
C. 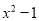 D.
D. 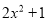
 C
【解析】根据平方差公式: ,可知因式分解为: .
故选:C.
C
【解析】根据平方差公式: ,可知因式分解为: .
故选:C. 下列多项式,能用公式法分解因式的有( )
①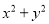 ②
②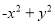 ③
③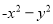 ④
④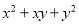
⑤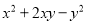 ⑥
⑥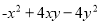
A. 2个 B. 3个 C. 4个 D. 5个
 A
【解析】根据完全平方公式,平方差公式,
的特征可判定②可以利用平方差公式进行因式分解,⑥可以利用完全平方公式进行因式分解,因此本题正确选项是A.
A
【解析】根据完全平方公式,平方差公式,
的特征可判定②可以利用平方差公式进行因式分解,⑥可以利用完全平方公式进行因式分解,因此本题正确选项是A. 如图,MN与PQ相交于点O,MO=OP,QO=ON,∠M=65°,∠Q=30°,则∠P=____,∠N=___.
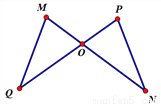
 65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30°
65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30° 使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条边对应相等
 D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错...
D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错... 填空:
(1)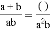 ; (2)
; (2)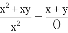 ;
;
(3)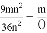 ; (4)
; (4)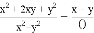 .
.
 ⑴,⑵x,⑶4n,⑷x-y.
【解析】(1)= ,
(2)= ,
(3)=,
(4)=.
故答案为:⑴a²+ab,⑵x,⑶4n,⑷x-y.
⑴,⑵x,⑶4n,⑷x-y.
【解析】(1)= ,
(2)= ,
(3)=,
(4)=.
故答案为:⑴a²+ab,⑵x,⑶4n,⑷x-y. 已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.求证:∠AHF=∠BGF.
 证明见解析.
【解析】试题分析:连接AC,取AC中点为M,连接ME、MF,根据中位线定理证明EM=MF,从而可得∠MEF=∠MFE,根据平行线同位角相等,证明∠MEF=∠AHF,∠MFE=∠BGF,可以求证∠AHF=∠BGF.
试题解析:连接AC,取AC中点为M,连接ME、MF,如图:
∵E是CD的中点,M为AC中点,
∴EM∥AD,且EM=AD,
∵M是AC的中点,...
证明见解析.
【解析】试题分析:连接AC,取AC中点为M,连接ME、MF,根据中位线定理证明EM=MF,从而可得∠MEF=∠MFE,根据平行线同位角相等,证明∠MEF=∠AHF,∠MFE=∠BGF,可以求证∠AHF=∠BGF.
试题解析:连接AC,取AC中点为M,连接ME、MF,如图:
∵E是CD的中点,M为AC中点,
∴EM∥AD,且EM=AD,
∵M是AC的中点,... 
