如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则tan∠A′BC′=________.

 【解析】过A′作出A′D⊥BC′,垂足为D,
在等腰直角三角形A′B′C′中,则A′D是底边上的中线,
∴B′C′=2 A′D,
∵BC=B′C′,
∴BD=BC+B′D=3 A′D,
∴ tan∠A′BC′=,
故答案为: .
【解析】过A′作出A′D⊥BC′,垂足为D,
在等腰直角三角形A′B′C′中,则A′D是底边上的中线,
∴B′C′=2 A′D,
∵BC=B′C′,
∴BD=BC+B′D=3 A′D,
∴ tan∠A′BC′=,
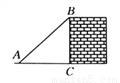
故答案为: . 如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=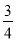 ,则梯子AB的长度为______米.
,则梯子AB的长度为______米.
 4
【解析】在Rt△BCA中,AC=3米,cos∠BAC=,所以AB=4米,即梯子的长度为4米.
4
【解析】在Rt△BCA中,AC=3米,cos∠BAC=,所以AB=4米,即梯子的长度为4米. 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′=________.
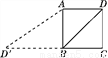
 【解析】由题知,∠ABD′=90°,BD=BD′==2,,
∴tan∠BAD′==,
故答案为: .
【解析】由题知,∠ABD′=90°,BD=BD′==2,,
∴tan∠BAD′==,
故答案为: . 一次函数的图象经过点(tan 45°,tan 60°)和(-cos 60°,-6tan 30°),则此一次函数的表达式为________.
 y=2x-
【解析】tan 45°=1,tan 60°=,-cos 60°=-,-6tan 30°=-2,
设y=kx+b的图象经过点(1, ),(- ,-2),
则有,解得: ,
∴一次函数解析式为: ,
故答案为: .
y=2x-
【解析】tan 45°=1,tan 60°=,-cos 60°=-,-6tan 30°=-2,
设y=kx+b的图象经过点(1, ),(- ,-2),
则有,解得: ,
∴一次函数解析式为: ,
故答案为: . 计算:
(1) 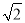 (2cos 45°-sin 60°)+
(2cos 45°-sin 60°)+ ;
;
(2)sin 60°·cos 60°-tan 30°·tan 60°+sin245°+cos245°.
 (1)2;(2)
【解析】试题分析:(1)先将特殊角的三角函数值代入,对最后一项的二次根式进行化简,然后再按运算顺序进行计算即可;
(2)将特殊角的三角函数值代入,按运算顺序进行计算即可得.
试题解析:(1)原式==2;
(2)原式=.
(1)2;(2)
【解析】试题分析:(1)先将特殊角的三角函数值代入,对最后一项的二次根式进行化简,然后再按运算顺序进行计算即可;
(2)将特殊角的三角函数值代入,按运算顺序进行计算即可得.
试题解析:(1)原式==2;
(2)原式=. 在△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)已知c=8 ,∠A=60°,求∠B,a,b;
,∠A=60°,求∠B,a,b;
(2)已知a=3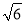 ,∠A=45°,求∠B,b,c.
,∠A=45°,求∠B,b,c.
 (1)∠B=30°,a=12,b=4;(2)∠B=45°,b=3,c=6.
【解析】试题分析:(1)根据直角三角形两锐角互余求得∠B的度数,再根据30度角所对直角边等于斜边一半求得b,再根据勾股定理求得a即可;
(2)先根据直角三角形两锐角互余求得∠B=45°,从而得到b=a,再利用勾股定理即可求得c.
试题解析:(1)∵∠C=90°,∠A=60°,∴∠B=90°-∠A=30°,...
(1)∠B=30°,a=12,b=4;(2)∠B=45°,b=3,c=6.
【解析】试题分析:(1)根据直角三角形两锐角互余求得∠B的度数,再根据30度角所对直角边等于斜边一半求得b,再根据勾股定理求得a即可;
(2)先根据直角三角形两锐角互余求得∠B=45°,从而得到b=a,再利用勾股定理即可求得c.
试题解析:(1)∵∠C=90°,∠A=60°,∴∠B=90°-∠A=30°,... 如图,已知?ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=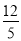 ,求CF的长.
,求CF的长.
 (1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边...
(1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边... 如图,拦水坝的横断面为等腰梯形ABCD,坝顶宽BC为6 m,坝高为3.2 m,为了提高水坝的拦水能力需要将水坝加高2 m,并且保持坝顶宽度不变,迎水坡CD的坡度不变,但是背水坡的坡度由原来的1∶2变成1∶2.5(坡度是坡高与坡的水平长度的比).求加高后的坝底HD的长为多少.

 29.4 m.
【解析】试题分析:应把所求的HD进行合理分割=HN+NF+FD,可利用Rt△MHN和Rt△EFD中的三角函数来做.
试题解析:由题意得BG=3.2 m,MN=EF=3.2+2=5.2(m),ME=NF=BC=6 m,
在Rt△DEF中,∵,
∴FD=2EF=2×5.2=10.4(m),
在Rt△HMN中,∵,
∴HN=2.5MN=13(m),
...
29.4 m.
【解析】试题分析:应把所求的HD进行合理分割=HN+NF+FD,可利用Rt△MHN和Rt△EFD中的三角函数来做.
试题解析:由题意得BG=3.2 m,MN=EF=3.2+2=5.2(m),ME=NF=BC=6 m,
在Rt△DEF中,∵,
∴FD=2EF=2×5.2=10.4(m),
在Rt△HMN中,∵,
∴HN=2.5MN=13(m),
... 小红家的阳台上放置了一个晒衣架(如图①),图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm(参考数据:sin 61.9°≈0.882,cos 61.9°≈0.471,tan 28.1°≈0.534).

(1)求证:AC∥BD.
(2)求扣链EF与立杆AB的夹角∠OEF的度数(结果精确到0.1°).
(3)小红的连衣裙穿在晒衣架上的总长度达到122 cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
 (1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
∴所以:小红的连衣裙垂挂在衣架后的总...
(1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
∴所以:小红的连衣裙垂挂在衣架后的总... 下列属于分式方程的是( )
A. 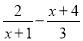 B.
B. 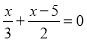
C. 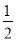 (x-1)=
(x-1)=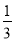 x D.
x D. 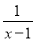 -x=1
-x=1
 D
【解析】试题解析:A,不是等式,所以不是方程,故不是分式方程.
B,C是一元一次方程,不是分式方程.
D.是分式方程.
故选D.
D
【解析】试题解析:A,不是等式,所以不是方程,故不是分式方程.
B,C是一元一次方程,不是分式方程.
D.是分式方程.
故选D.