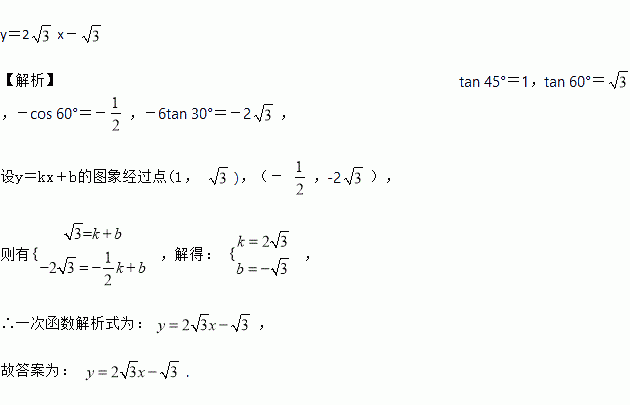题目内容
一次函数的图象经过点(tan 45°,tan 60°)和(-cos 60°,-6tan 30°),则此一次函数的表达式为________.
 y=2x-
【解析】tan 45°=1,tan 60°=,-cos 60°=-,-6tan 30°=-2,
设y=kx+b的图象经过点(1, ),(- ,-2),
则有,解得: ,
∴一次函数解析式为: ,
故答案为: .
y=2x-
【解析】tan 45°=1,tan 60°=,-cos 60°=-,-6tan 30°=-2,
设y=kx+b的图象经过点(1, ),(- ,-2),
则有,解得: ,
∴一次函数解析式为: ,
故答案为: .
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a-b<0,则下列各式中一定正确的是( )
A、a>b B、ab>0 C、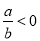 D、-a>-b
D、-a>-b
 D
【解析】
试题分析:由a-b<0可得a<b,再根据不等式的基本性质依次分析各项即可.
a-b<0,
∴a<b,
∴-a>-b,但无法确定ab与的符号,
故选D.
D
【解析】
试题分析:由a-b<0可得a<b,再根据不等式的基本性质依次分析各项即可.
a-b<0,
∴a<b,
∴-a>-b,但无法确定ab与的符号,
故选D. 老师拿出6根小木棒,3根长的相同,3根短的也相同,且长的是短的的长度的2倍,请用这6根木棒摆成四个完全相同的三角形.
 见解析
【解析】试题分析:用3根长的构成一个大等边三角形,3根短的构成一个小等边三角形即可.
试题解析:【解析】
如图.
见解析
【解析】试题分析:用3根长的构成一个大等边三角形,3根短的构成一个小等边三角形即可.
试题解析:【解析】
如图. 分式方程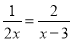 的解是_____.
的解是_____.
 x=﹣1
【解析】试题分析:根据解分式方程的方法可以求得分式方程的解,记住最后要进行检验,本题得以解决.
【解析】
方程两边同乘以2x(x﹣3),得
x﹣3=4x
解得,x=﹣1,
检验:当x=﹣1时,2x(x﹣3)≠0,
故原分式方程的解是x=﹣1,
故答案为:x=﹣1.
x=﹣1
【解析】试题分析:根据解分式方程的方法可以求得分式方程的解,记住最后要进行检验,本题得以解决.
【解析】
方程两边同乘以2x(x﹣3),得
x﹣3=4x
解得,x=﹣1,
检验:当x=﹣1时,2x(x﹣3)≠0,
故原分式方程的解是x=﹣1,
故答案为:x=﹣1. 小红家的阳台上放置了一个晒衣架(如图①),图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm(参考数据:sin 61.9°≈0.882,cos 61.9°≈0.471,tan 28.1°≈0.534).

(1)求证:AC∥BD.
(2)求扣链EF与立杆AB的夹角∠OEF的度数(结果精确到0.1°).
(3)小红的连衣裙穿在晒衣架上的总长度达到122 cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
 (1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
∴所以:小红的连衣裙垂挂在衣架后的总...
(1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
∴所以:小红的连衣裙垂挂在衣架后的总... 如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC对称,若DM=1,则tan∠ADN=________.
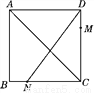
 【解析】试题分析:在正方形ABCD中,AB=CD.由M、N两点关于对角线AC对称,所以DM=BN=1, 再由题意可知tan∠AND===tan(90°-∠CDN),进而求出CN=BC-BN=4-1=3.再由题意可知tan∠AND=tan(90°-∠CDN)===.
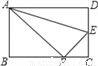
【解析】试题分析:在正方形ABCD中,AB=CD.由M、N两点关于对角线AC对称,所以DM=BN=1, 再由题意可知tan∠AND===tan(90°-∠CDN),进而求出CN=BC-BN=4-1=3.再由题意可知tan∠AND=tan(90°-∠CDN)===. 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
A. 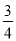 B.
B. 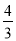 C.
C. 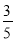 D.
D. 
 A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A.
A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A. 把多项式-x2+x提取公因式-x后,余下的部分是( )
A. x B. x-1 C. x+1 D. x2
 B
【解析】根据因式分解的提公因式,提取公因式-x,可得-x2+x=-x(x-1),所以剩余部分为x-1.
故选:B.
B
【解析】根据因式分解的提公因式,提取公因式-x,可得-x2+x=-x(x-1),所以剩余部分为x-1.
故选:B. 将一副直角三角尺如图放置,若∠AOD=20°, 则∠BOC的大小为( )
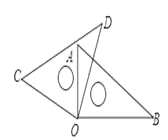
A. 140° B. 160° C. 170° D. 150°
 B
【解析】试题分析:根据∠AOD=20°可得:∠AOC=70°,根据题意可得:∠BOC=∠AOB+∠AOC=90°+70°=160°.
B
【解析】试题分析:根据∠AOD=20°可得:∠AOC=70°,根据题意可得:∠BOC=∠AOB+∠AOC=90°+70°=160°.