题目内容
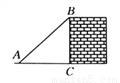
如图所示，一架梯子斜靠在墙上，若梯子底端到墙的距离AC=3米，cos∠BAC＝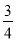
，则梯子AB的长度为______米．
4
【解析】在Rt△BCA中，AC＝3米，cos∠BAC＝，所以AB＝4米，即梯子的长度为4米．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长．
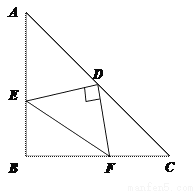
连结BD，证△BED≌△CFD和△AED≌△BFD，得BF=4，BE=3，再运用勾股定理求得EF=5 将点A绕另一个点O旋转一周，点A在旋转过程中所经过的路线是_______.
圆
【解析】
试题分析：根据圆的定义，到定点的距离等于定长的点的轨迹是圆．
依题意，点A绕点O旋转一周的路线是圆． 若关于x的方程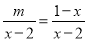
有增根，则m的值为( )
A. 0 B. 1 C. －1 D. 2
C
【解析】试题解析：方程两边同乘以x?2，得
①
∵原方程有增根，
∴x?2=0，
即x=2.
把x=2代入①，得
m=?1.
故选C. 如图，已知?ABCD，点E是BC边上的一点，将边AD延长至点F，使∠AFC＝∠DEC.
(1)求证：四边形DECF是平行四边形；
(2)若AB＝13，DF＝14，tan A＝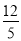
，求CF的长．
（1）见解析；（2）15
【解析】 试题分析：（1）由已知可知AD∥BC，从而得∠ADE＝∠DEC，再根据∠AFC＝∠DEC，从而得∠AFC＝∠ADE，继而得DE∥FC，问题得证；
（2）过点D作DH⊥BC于点H，由已知得到∠BCD＝∠A，AB＝CD＝13，再根据tan A＝tan∠DCH＝，从而得到DH、CH的长，从而得到CE、DE的长，继而得CF的长.
试题解析：（1）∵四边... 在△ABC中，∠C＝90°，AB＝13，BC＝5，则tanB＝________．
【解析】∵∠C=90°，AB=13，BC=5，∴AC==12，∴tanB=，
故答案为： . 如图，在四边形ABCD中，AD∥BC，AC⊥AB，AD=CD，cos ∠DCA=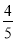
，BC=10，则AB的值是( )
A. 3 B. 6 C. 8 D. 9
B
【解析】∵AD∥BC，∴∠DAC＝∠ACB．∵AD＝CD，
∴∠DAC＝∠DCA．∴∠ACB＝∠DCA．
∴，即，∴AC＝8，
∴． 多项式15m3n2+5m2n﹣20m2n3的公因式是（ ）
A. 5mn B. 5m2n2 C. 5m2n D. 5mn2
C
【解析】多项式15n²+5m²n?20m² 中，
各项系数的最大公约数是5，
各项都含有的相同字母是m、n，字母m的指数最低是2，字母n的指数最低是1，
所以它的公因式是5m²n.
故选C. 如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过点E作AC的垂线，交CD的延长线于点F．求证：AB=FC．
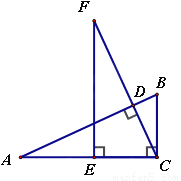
见解析证明．
【解析】
试题分析：利用同角的余角相等得到一对角相等，再由一对直角相等，夹边EC=BC，利用AAS得到△FEC与△ACB全等，利用全等三角形对应边相等即可得证．
试题解析：∵EF⊥AC，∴∠FEC=90°=∠ACB，∴∠F +∠FCE= 90°，∵CD⊥AB，∴∠ADC=90°，∴∠A +∠FCE =90°， ∴∠F=∠A，在△FEC和△ACB中，∵，∴△FEC≌△...