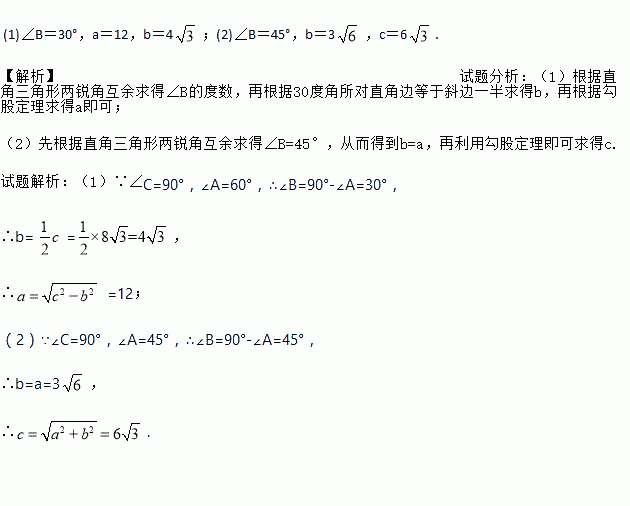��Ŀ����
�ڡ�ABC�У���C��90�㣬��A����B����C���Եı߷ֱ�Ϊa��b��c.
(1)��֪c��8 ����A��60�㣬���B��a��b��
����A��60�㣬���B��a��b��
(2)��֪a��3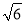 ����A��45�㣬���B��b��c.
����A��45�㣬���B��b��c.
 (1)��B��30�㣬a��12��b��4��(2)��B��45�㣬b��3��c��6.
�������������������1������ֱ������������ǻ�����á�B�Ķ������ٸ���30�Ƚ�����ֱ�DZߵ���б��һ�����b���ٸ��ݹ��ɶ������a���ɣ�
��2���ȸ���ֱ������������ǻ�����á�B=45�㣬�Ӷ��õ�b=a�������ù��ɶ����������c.
�����������1���ߡ�C=90�㣬��A=60�㣬���B=90��-��A=30�㣬...
(1)��B��30�㣬a��12��b��4��(2)��B��45�㣬b��3��c��6.
�������������������1������ֱ������������ǻ�����á�B�Ķ������ٸ���30�Ƚ�����ֱ�DZߵ���б��һ�����b���ٸ��ݹ��ɶ������a���ɣ�
��2���ȸ���ֱ������������ǻ�����á�B=45�㣬�Ӷ��õ�b=a�������ù��ɶ����������c.
�����������1���ߡ�C=90�㣬��A=60�㣬���B=90��-��A=30�㣬...
���t��0����ôa��t��a�Ĵ�С��ϵ�ǣ� ��
A��a��t��a B��a��t��a C��a��t��a D������ȷ��
 A
��������
������������ݲ���ʽ�Ļ������ʼ��ɵõ����.
t��0��
��a��t��a��
��ѡA.
A
��������
������������ݲ���ʽ�Ļ������ʼ��ɵõ����.
t��0��
��a��t��a��
��ѡA. ��ͼ��ʾ���ĸ�ͼ���У��Ӽ���ͼ�α任�ĽǶȿ��ǣ���һ��������������ͬ?��ָ�����ͼ�Σ�������������ɣ�
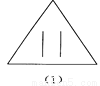
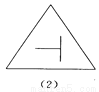
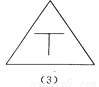
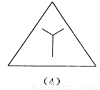
 ͼ(2)������������Գ�ͼ��
������������������۲�ͼ�η��֣�1����3����4��������Գ�ͼ�Σ�����2��������Գ�ͼ�Σ��ɴ˼��ɵó����ۣ�
�����������������
��1����3����4��������Գ�ͼ�Σ�����2��������Գ�ͼ�Σ��ʴӼ���ͼ�α任�ĽǶȿ��ǣ�ͼ��2��������������ͬ��
ͼ(2)������������Գ�ͼ��
������������������۲�ͼ�η��֣�1����3����4��������Գ�ͼ�Σ�����2��������Գ�ͼ�Σ��ɴ˼��ɵó����ۣ�
�����������������
��1����3����4��������Գ�ͼ�Σ�����2��������Գ�ͼ�Σ��ʴӼ���ͼ�α任�ĽǶȿ��ǣ�ͼ��2��������������ͬ�� �ⷽ�̣�
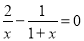
 x����2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
ȥ���ţ���
�����
�ϲ�ͬ�����
���飺��ʱ��
��ԭ���̵Ľ�.
x����2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
ȥ���ţ���
�����
�ϲ�ͬ�����
���飺��ʱ��
��ԭ���̵Ľ�. ����x�ķ���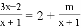 �⣬��m��ֵΪ��������
�⣬��m��ֵΪ��������
A. ��5 B. ��8 C. ��2 D. 5
 A
�����������������ȥ��ĸ�ã�3x��2=2x+2+m���ɷ�ʽ�����⣬�õ�x+1=0����x=��1��������ʽ���̵ã���5=��2+2+m����ã�m=��5����ѡA��
A
�����������������ȥ��ĸ�ã�3x��2=2x+2+m���ɷ�ʽ�����⣬�õ�x+1=0����x=��1��������ʽ���̵ã���5=��2+2+m����ã�m=��5����ѡA�� ��ͼ������AΪֱ�Ƕ���ĵ���ֱ��������ABC��ֱ��BCƽ�Ƶõ���A��B��C�䣬ʹ��B����C�غϣ�����A��B����tan��A��BC�䣽________.

 ����������A������A��D��BC�䣬����ΪD��
�ڵ���ֱ��������A��B��C���У���A��D�ǵױ��ϵ����ߣ�
��B��C��=2 A��D��
��BC=B��C�䣬
��BD=BC+B��D=3 A��D��
�� tan��A��BC��=��
�ʴ�Ϊ�� .
����������A������A��D��BC�䣬����ΪD��
�ڵ���ֱ��������A��B��C���У���A��D�ǵױ��ϵ����ߣ�
��B��C��=2 A��D��
��BC=B��C�䣬
��BD=BC+B��D=3 A��D��
�� tan��A��BC��=��
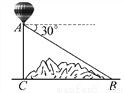
�ʴ�Ϊ�� . ��ͼ��ij�������ٹ�·��Ҫ��B����C����һ������(B��C��ͬһˮƽ����)��Ϊ�˲���B��C����֮��ľ��룬ij����ʦ�����������C�س�������ֱ����100m����A������A���۲�B�صĸ���Ϊ30�㣬��B��C����֮��ľ���Ϊ( )
A. 100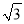 m B. 50
m B. 50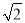 m C. 50
m C. 50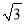 m D.
m D. 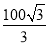 m
m
 A
�������������������������ã���ABC=30�㣬AC��BC��AC=100m��
��Rt��ABC��BC=��m����
��ѡA��
A
�������������������������ã���ABC=30�㣬AC��BC��AC=100m��
��Rt��ABC��BC=��m����
��ѡA�� ��9a2b��3ac2��6abc����Ĺ���ʽ��_______��
 ��3a
�������������ṫ��ʽ����ʽ�ֽ⣬��֪��������Ϊ�������Ķ���ʽ����˿�֪�乫��ʽΪ-3a.
�ʴ�Ϊ��-3a.
��3a
�������������ṫ��ʽ����ʽ�ֽ⣬��֪��������Ϊ�������Ķ���ʽ����˿�֪�乫��ʽΪ-3a.
�ʴ�Ϊ��-3a. ��ͼ��һ������ֽƬ����ȥ���ֺ�õ�һ�������Σ���ͼ�С�1+��2�Ķ����ǣ� ��
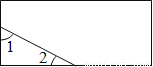
A. 30�� B. 60�� C. 90�� D. 120��
 C
�����������������������ã�ʣ�µ���������ֱ�������Σ�
���ԣ���1+��2=90�㣮
��ѡC��
C
�����������������������ã�ʣ�µ���������ֱ�������Σ�
���ԣ���1+��2=90�㣮
��ѡC��