��Ŀ����
��ͼ����ˮ�ӵĺ����Ϊ��������ABCD���Ӷ���BCΪ6 m���Ӹ�Ϊ3.2 m��Ϊ�����ˮ�ӵ���ˮ������Ҫ��ˮ�ӼӸ�2 m�����ұ��ְӶ����Ȳ��䣬ӭˮ��CD���¶Ȳ��䣬���DZ�ˮ�µ��¶���ԭ����1��2���1��2.5(�¶����¸����µ�ˮƽ���ȵı�)����Ӹߺ�İӵ�HD�ij�Ϊ���٣�

 29.4 m.
�����������������Ӧ�������HD���к����ָ�=HN+NF+FD��������Rt��MHN��Rt��EFD�е����Ǻ���������
����������������BG��3.2 m��MN��EF��3.2��2��5.2(m)��ME��NF��BC��6 m��
��Rt��DEF�У��ߣ�
��FD��2EF��2��5.2��10.4(m)��
��Rt��HMN�У��ߣ�
��HN��2.5MN��13(m)��
...
29.4 m.
�����������������Ӧ�������HD���к����ָ�=HN+NF+FD��������Rt��MHN��Rt��EFD�е����Ǻ���������
����������������BG��3.2 m��MN��EF��3.2��2��5.2(m)��ME��NF��BC��6 m��
��Rt��DEF�У��ߣ�
��FD��2EF��2��5.2��10.4(m)��
��Rt��HMN�У��ߣ�
��HN��2.5MN��13(m)��
...
 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д���֪������a��b��c�������ϵ�λ����ͼ��ʾ��������ʽ����ȷ���ǣ� ��
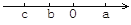
A. cb��ab B. ac��ab C. cb��ab D. c��b��a��b
 A
������������������ȸ���������ص�ó�a��0��b��c���ٸ��ݲ���ʽ�����ʽ����жϣ�
A����a��0��b��c����cb��0��ab. ѡ����ȷ.
B����c��b��a��0����ac��ab. ѡ�����.
C����c��a��b��0����cb��ab. ѡ�����.
D����c��a����c+b��a+b. ѡ�����.
��ѡA��
A
������������������ȸ���������ص�ó�a��0��b��c���ٸ��ݲ���ʽ�����ʽ����жϣ�
A����a��0��b��c����cb��0��ab. ѡ����ȷ.
B����c��b��a��0����ac��ab. ѡ�����.
C����c��a��b��0����cb��ab. ѡ�����.
D����c��a����c+b��a+b. ѡ�����.
��ѡA�� ���߶�AB��CD����AB��CD���ഹֱƽ�֣�����ΪO��AB��2CD���ֱ�ȡOA��OB��OC��OD���е�A�䡢B�䡢C�䡢D�䣬����CA�䡢DA�䡢CB�䡢DB�䡢AC�䡢AD�䡢BC�䡢BD��õ�һ���Ľ���ͼ���������Ľ�����ˮƽ��������ƽ��2���ף�����ƽ��ǰ���ͼ�Σ�
 ������
��������������������ݴ�ֱƽ���ߵ����壬���߶�AB��4���ף�����AB�Ĵ�ֱƽ���߶�CD��2���ף���AB�ڵ�O���ٷֱ�ȡOA��OB��OC��OD���е�A�䡢B�䡢C�䡢D�䣬����CA�䡢DA�䡢CB�䡢DB�䡢AC�䡢AD�䡢BC�䡢BD��õ�һ���Ľ���ͼ��A��B��C��D�䣻�ٸ���ƽ��ͼ�ε����������Ľ���ͼ��A��B��C��D����ĸ�����ֱ�����ƽ��2���ף�����β������㣬���ɵõ��Ľ���ͼ��...
������
��������������������ݴ�ֱƽ���ߵ����壬���߶�AB��4���ף�����AB�Ĵ�ֱƽ���߶�CD��2���ף���AB�ڵ�O���ٷֱ�ȡOA��OB��OC��OD���е�A�䡢B�䡢C�䡢D�䣬����CA�䡢DA�䡢CB�䡢DB�䡢AC�䡢AD�䡢BC�䡢BD��õ�һ���Ľ���ͼ��A��B��C��D�䣻�ٸ���ƽ��ͼ�ε����������Ľ���ͼ��A��B��C��D����ĸ�����ֱ�����ƽ��2���ף�����β������㣬���ɵõ��Ľ���ͼ��... ���ʽ���̣�
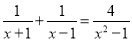
 x��2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
�����
�ϲ�ͬ�����
ϵ����Ϊ1����
���飺��ʱ��
��ԭ���̵Ľ�.
x��2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
�����
�ϲ�ͬ�����
ϵ����Ϊ1����
���飺��ʱ��
��ԭ���̵Ľ�. ���ʽ����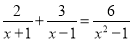 ���������IJ������У������һ����( )
���������IJ������У������һ����( )
A. �������߷�ʽ�����ĸ�ǣ�x�C1����x+1��
B. �������߶����ԣ�x�C1����x+1��������ʽ����2��x�C1��+3��x+1��=6
C. �������ʽ���̣���x=1
D. ԭ���̵Ľ�Ϊx=1
 D
����������������������⣬��Ȼ������ã����ǽ�����ԭ�����У��ɷ��ֺ͵ķ�ĸ��Ϊ�㣬�������壬���ԣ���������
D
����������������������⣬��Ȼ������ã����ǽ�����ԭ�����У��ɷ��ֺ͵ķ�ĸ��Ϊ�㣬�������壬���ԣ��������� ��ͼ����֪������ABCD�ı߳�Ϊ2��������߶�BD���ŵ�B��ת��D����CB���ӳ����ϵ�D�䴦����ôtan��BAD�䣽________.
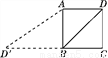
 ������������֪����ABD��=90�㣬BD=BD��==2����
��tan��BAD��==��
�ʴ�Ϊ�� .
������������֪����ABD��=90�㣬BD=BD��==2����
��tan��BAD��==��
�ʴ�Ϊ�� . ��ͼ����ij����B������һ��������ҵ���洬����ƫ��15�㷽���A�������洬�ر�ƫ��75�㷽����40����/Сʱ���ٶȺ��У����а�Сʱ��C������C���۲B��C�ı�ƫ��60�㷽���ϣ���B��C֮��ľ���Ϊ��������
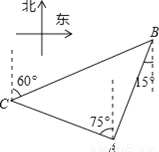
A. 20���� B. 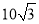 ���� C. 20
���� C. 20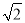 ���� D. 30����
���� D. 30����
 C
���������ߡ�ABE��15�㣬AD��BE��
���DAB����ABE��15�㣬
���CAB����CAD����DAB��90�㣮
�ߡ�FCB��60�㣬CF��BE��
���CBE����FCB��60�㣮
�֡�CBA����ABE����CBE��
���CBA��45�㣮
��Rt��ABC��
��
��ú��
��ѡC��
C
���������ߡ�ABE��15�㣬AD��BE��
���DAB����ABE��15�㣬
���CAB����CAD����DAB��90�㣮
�ߡ�FCB��60�㣬CF��BE��
���CBE����FCB��60�㣮
�֡�CBA����ABE����CBE��
���CBA��45�㣮
��Rt��ABC��
��
��ú��
��ѡC�� ��ʽ�֡�������
x2��3x =______________.
 x(x-3)
�������������������ȡ����ʽx���ɣ���x2��3x=x��x��3����
x(x-3)
�������������������ȡ����ʽx���ɣ���x2��3x=x��x��3���� ���п�ʹ����ֱ��������ȫ�ȵ������ǣ�������
A. һ���߶�Ӧ��� B. ����ֱ�DZ߶�Ӧ���
C. һ����Ƕ�Ӧ��� D. ������Ƕ�Ӧ���
 B
����������������
��ֱ������������һ����������ֱ����ȣ�Ҫ�ж���ֱ��������ȫ�ȣ����뻹Ҫ�����������ʿ��ų�A��C��
��D������AAA�������ж�ȫ�ȣ�
B������SAS�������ж�����ֱ��������ȫ�ȣ�
��ѡB��
B
����������������
��ֱ������������һ����������ֱ����ȣ�Ҫ�ж���ֱ��������ȫ�ȣ����뻹Ҫ�����������ʿ��ų�A��C��
��D������AAA�������ж�ȫ�ȣ�
B������SAS�������ж�����ֱ��������ȫ�ȣ�
��ѡB�� 
