题目内容
如图，已知?ABCD，点E是BC边上的一点，将边AD延长至点F，使∠AFC＝∠DEC.
(1)求证：四边形DECF是平行四边形；
(2)若AB＝13，DF＝14，tan A＝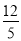
，求CF的长．
（1）见解析；（2）15
【解析】 试题分析：（1）由已知可知AD∥BC，从而得∠ADE＝∠DEC，再根据∠AFC＝∠DEC，从而得∠AFC＝∠ADE，继而得DE∥FC，问题得证；
（2）过点D作DH⊥BC于点H，由已知得到∠BCD＝∠A，AB＝CD＝13，再根据tan A＝tan∠DCH＝，从而得到DH、CH的长，从而得到CE、DE的长，继而得CF的长.
试题解析：（1）∵四边...
练习册系列答案
相关题目
如果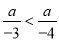
，则a必须满足（ ）
A、a≠0 B、a＜0 C、a＞0 D、a为任意数
C
【解析】
试题分析：根据不等式的基本性质即可判断.
，
∴a＞0，
故选C. 你能用一张长方形的纸片折出一个正三角形吗？动手试一试，简单叙述你的折法．
如图，先把矩形纸片对折，然后在沿着BM对折使C落在EF上的N点，再折出BM和CN即可．
【解析】试题分析：把长方形纸片ABCD的宽对折，然后展开，折痕记为EF，再把AD边折起，点D折叠到EF上，与EF的重合点为M，在CD上的折痕为点G，再沿GM对折，在AB上的折痕为H，则三角形AHG就是一个正三角形．
试题解析：【解析】
如图，
连接AM，在△AMG和△AMH中，
AM=... 解方程：
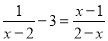
x＝3
【解析】试题分析：按照解分式方程的步骤解方程即可.
试题解析：去分母，得
去括号，得
移项，得
合并同类项，得
系数化为1，得
检验：当时，
是原方程的解. 分式方程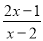
=1的解为（ ）
A. x=﹣1 B. x=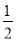
C. x=1 D. x=2
A
【解析】【解析】
去分母得：2x﹣1=x﹣2，
解得：x=﹣1，
经检验x=﹣1是分式方程的解，
则分式方程的解为x=﹣1．
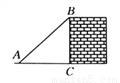
故选：A． 如图所示，一架梯子斜靠在墙上，若梯子底端到墙的距离AC=3米，cos∠BAC＝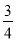
，则梯子AB的长度为______米．
4
【解析】在Rt△BCA中，AC＝3米，cos∠BAC＝，所以AB＝4米，即梯子的长度为4米． 等腰三角形一腰上的高与腰长之比是1?2，则等腰三角形顶角的度数为( )
A. 30° B. 50° C. 60°或120° D. 30°或150°
D
【解析】如图1，当高BD在三角形的内部时，
∵高BD是腰长AB的一半，
∴sin A＝，∴∠A＝30°；
如图2，当高CD在三角形的外部时，
∵高CD是腰长AC的一半，
∴sin∠1＝，∴∠1＝30°，
∴∠BAC=180°-30°=150°，
∴该三角形的顶角的度数是30°或150°，
故选D． 4x(m－n)＋8y(n－m)2中各项的公因式是________.
4(m－n)
【解析】根据题意，先变形为4x(m－n)＋8y(m－n)2，把m-n看做一个整体，即可找到公因式4（m-n）.
故答案为：4（m-n）. 如图，若要用“HL”证明Rt△ABC≌Rt△ABD，则还需补充条件（ ）
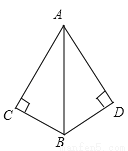
A. ∠BAC=∠BAD B. AC=AD或BC=BD
C. AC=AD且BC=BD D. 以上都不正确
B
【解析】试题解析：从图中可知AB为Rt△ABC和Rt△ABD的斜边，也是公共边．
很据“HL”定理，证明Rt△ABC≌Rt△ABD，
还需补充一对直角边相等，
即AC=AD或BC=BD，
故选B．